算法设计与分析

发表于 2020-05-17 更新于 2023-04-08 分类于 cs ， data-structure 阅读次数：本文字数： 4.8k 阅读时长 ≈ 17 分钟

本文主要介绍了算法的一些特性和常见算法的实现方法。其中，时间复杂度是算法效率的重要指标，递归是一种常见的算法实现方式，分治法、动态规划、贪心算法和回溯法是常见的算法设计思想。此外，还介绍了哈夫曼编码、单源最短路径、最小生成树、并查集和优先队列等常见算法的实现方法和应用场景。这些算法在计算机科学和工程领域中都有广泛的应用，对于提高算法效率和解决实际问题具有重要意义。

算法设计与分析

算法的特性

定义

为了解决某类问题而规定的一个有限长的操作序列。

算法的特性

有穷性，确定性，可行性，输入，输出

算法的性能标准

正确性、可读性、健壮性、高效率和低存储需求

时间复杂度

常见算法时间复杂度

\(O(1)\): 表示算法的运行时间为常量
\(O(n)\): 表示该算法是线性算法
\(O(logn)\): 二分查找算法
\(O(n^2)\): 对数组进行排序的简单算法，如直接插入排序。
\(O(n^3)\): 做两个n阶矩阵的乘法运算
\(O(2^n)\): 求具有n个元素集合的所有子集的算法
\(O(n!)\): 求具有n个元素的全排列的算法

算法复杂性分析

\[ f(n)=O(g(n)) \qquad f(n)的阶≤g(n)的阶\\ f(n)=Ω(g(n)) \qquad f(n)的阶≥g(n)的阶\\ f(n)=θ(g(n)) \qquad f(n)的阶＝g(n)的阶\\ f(n)=o(g(n)) \qquad f(n)的阶＜g(n)的阶\\ \]

递归

二分查找（递归）

int binary_search(int* a, int left, int right, int target){
    if(left > right) return -1;
    int mid = (left + right) / 2;
    if(a[mid] == target) return mid;
    if(a[mid] < target) return binary_search(a, mid + 1, right, target);
    else return binary_search(a, left, mid - 1, target);
}

二分查找（非递归）

int binary_search(int* a, int left, int right, int target){
    while(left <= right){
        int mid = (left + right) / 2;
        if(a[mid] == target) return mid;
        if(a[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

快速排序

选择划分基准 a(p)
将数组 a 划分成两个子数组，使得 a[l...p-1] <= a(p)，a[p+1...r] >= a(p)
递归调用快速排序算法，对 a[l...p-1] 和 a[p+1...r] 进行排序

递归

C参考实现

void quickSort(int* a, int left, int right){
    int i = left, j = right, base = a[left], tmp;
    if(left >= right) return;
    while(i != j){
        while(a[j] >= base && i < j) j--;
        while(a[i] <= base && i < j) i++;
        if(i < j) tmp = a[i], a[i] = a[j], a[j] = tmp;
    }
    a[left] = a[i], a[i] = base;
    quickSort(a, left, i - 1);
    quickSort(a, i + 1, right);
}

Java参考实现

public class QuickSort {
    private static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    private static int partition(int[] arr, int left, int right){
        int j = left - 1;
        for(int i = left; i < right; i++)
            if (arr[i] < arr[right]) swap(arr, i, ++j);
        swap(arr, right, ++j);
        return j;
    }

    public static void sort(int[] arr, int left, int right){
        if(left < right){
            int index = partition(arr, left, right);
            sort(arr, left, index - 1);
            sort(arr, index + 1, right);
        }
    }

    public static void main(String[] args){
        int[] arr = {4, 8, 2, 1, 5, 6, 7, 9, 3};
        sort(arr, 0, arr.length - 1);
        for (int x: arr) System.out.print(x + " ");
    }
}

非递归

import java.util.LinkedList;

public class QuickSort2 {
    private static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    private static int partition(int[] arr, int left, int right){
        int j = left - 1;
        for(int i = left; i < right; i++)
            if(arr[i] < arr[right]) swap(arr, i, ++j);
        swap(arr, right, ++j);
        return j;
    }

    public static void sort(int[] arr, int left, int right){
        if (left >= right) return;
        LinkedList<Integer> stack = new LinkedList<>();
        stack.push(left);
        stack.push(right);
        while (!stack.isEmpty()){
            int end = stack.pop();
            int begin = stack.pop();
            if (begin < end){
                int index = partition(arr, begin, end);
                stack.push(begin);
                stack.push(index - 1);
                stack.push(index + 1);
                stack.push(end);
            }
        }
    }

    public static void main(String[] args){
        int[] arr = new int[]{3, 1, 4, 9, 6, 0, 7, 2, 5, 8};
        sort(arr, 0, arr.length - 1);
        for (int e: arr) System.out.print(e + " ");
    }
}

分治法

基本思想

将求解的较大规模的问题分割成 k 个更小规模的子问题。对这 k 个子问题分别求解。如果子问题的规模仍然不够小，则再划分为 k 个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

适用条件

分治法所能解决的问题一般具有以下几个特征：

该问题的规模缩小到一定的程度就可以容易地解决；
该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
利用该问题分解出的子问题的解可以合并为该问题的解；
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

归并排序

其基本思想是：将待排序元素分成大小大致相同的 2 个子集合，分别对 2 个子集合进行排序，最终将排好序的子集合合并成为所要求的排好序的集合。

void merge(int* a, int x, int mid, int y, int* tmp){
    int i = x, j = mid + 1, t = 0;
    while(i <= mid && j <= y) tmp[t++] = a[i] <= a[j] ? a[i++] : a[j++];
    while(i <= mid) tmp[t++] = a[i++];
    while(j <= y) tmp[t++] = a[j++];
    t = 0;
    while(x <= y) a[x++] = tmp[t++];
}

void sort(int* a, int x, int y, int* tmp){
    if(x < y){
        int mid = (x + y) / 2;
        sort(a, x, mid, tmp);
        sort(a, mid + 1, y, tmp);
        merge(a, x, mid, y, tmp);
    }
}

求逆序对数

考虑 \(1,2,…,n\) 的排列 \(i1，i2，…，in\)，如果其中存在 \(j,k\)，满足 \(j < k\) 且 \(i_j > i_k\)，那么就称 \((i_j,i_k)\) 是这个排列的一个逆序。

一个排列含有逆序的个数称为这个排列的逆序数。例如排列 263451 含有8个逆序 (2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1)，因此该排列的逆序数就是 8。显然，由 1,2,…,n 构成的所有 n! 个排列中，最小的逆序数是 0，对应的排列就是 1,2,…,n；最大的逆序数是 n(n-1)/2，对应的排列就是 n,(n-1),…,2,1。逆序数越大的排列与原始排列的差异度就越大。

基本思路：

1.使用二分归并（分治法）进行求解； 2.将序列依此划分为两两相等的子序列； 3.对每个子序列进行排序（比较 a[i] > a[j]，如果满足条件，则求该子序列的逆序数 count = mid - i + 1，其中 mid = (left + right) / 2） 4.接着合并子序列即可。

void merge(int* a, int left, int mid, int right, int* tmp){
    int i = left, j = mid + 1, t = 0;
    while(i <= mid && j <= right){
        if(a[i] <= a[j]) tmp[t++] = a[i++];
        else{
            tmp[t++] = a[j++];
            count += mid - i + 1;
        }
    }
    while(i <= mid) tmp[t++] = a[i++];
    while(j <= right) tmp[t++] = a[j++];
    t = 0;
    while(left <= right) a[left++] = tmp[t++];
}

void mergeSort(int* a, int left, int right, int* tmp){
    if(left < right){
        int mid = (left + right) / 2;
        mergeSort(a, left, mid, tmp);
        mergeSort(a, mid + 1, right, tmp);
        merge(a, left, mid, right, tmp);
    }
}

快速选择算法

基本思想：

快速选择的总体思路与快速排序一致，选择一个元素作为基准来对元素进行分区，将小于和大于基准的元素分在基准左边和右边的两个区域。不同的是，快速选择并不递归访问双边，而是只递归进入一边的元素中继续寻找。这降低了平均时间复杂度，从 \(O(nlogn)\) 至 \(O(n)\)，不过最坏情况仍然是 \(O(n^2)\)。

int partition(int* a, int left, int right){
    int j = left - 1, tmp;  // 选择a[right]作为划分基准
    for(int i = left; i < right; i++){
        if(a[i] <= a[right]) tmp = a[i], a[i] = a[++j], a[j] = tmp;
    }
    tmp = a[right], a[right] = a[++j], a[j] = tmp;
    return j;
}

int quick_select(int* a, int left, int right, int k){
    if(left == right) return a[left];
    int idx = partition(a, left, right), cur = idx - left + 1;
    if(k == cur) return a[idx];
    else if(k < cur) return quick_select(a, left, idx - 1, k);
    else return quick_select(a, idx + 1, right, k - cur);
}

线性时间选择（BFPRT）

基本思路：

首先把数组按 5 个数为一组进行分组，最后不足 5 个的忽略。对每组数进行排序（如插入排序）求取其中位数。
把上一步的所有中位数移到数组的前面，对这些中位数递归调用 BFPRT 算法求得他们的中位数。
将上一步得到的中位数作为划分的主元进行整个数组的划分。
判断第k个数在划分结果的左边、右边还是恰好是划分结果本身，前两者递归处理，后者直接返回答案。

void bubble_sort(int* a, int left, int right){
    int tmp;
    for(int i = left; i < right; i++){
        for(int j = right; j > i; j--){
            if(a[j] < a[j-1]) tmp = a[j], a[j] = a[j-1], a[j-1] = tmp;
        }
    }
}

int partition(int* a, int left, int right, int baseIdx){
    int j = left - 1, tmp;
    // 将基准放于数组尾部
    tmp = a[right], a[right] = a[baseIdx], a[baseIdx] = tmp;
    for(int i = left; i < right; i++){
        if(a[i] <= a[right]) tmp = a[i], a[i] = a[++j], a[j] = tmp;
    }
    tmp = a[right], a[right] = a[++j], a[j] = tmp;
    return j;
}

int bfprt(int* a, int left, int right, int k){
    if(right - left + 1 <= 5){  // 小于等于5个数，直接排序得到结果
        bubble_sort(a, left, right);
        return a[left + k - 1];
    }
    int t = left - 1, tmp;  // t:当前替换到前面的中位数的下标
    for(int st = left, ed; (ed = st + 4) <= right; st += 5){
        bubble_sort(a, st, ed);
        // 将中位数替换到数组前面，便于递归求取中位数的中位数
        tmp = a[++t], a[t] = a[st+2], a[st+2] = tmp;
    }
    int baseIdx = (left + t) >> 1; // left到t的中位数的下标，作为主元的下标
    bfprt(a, left, t, baseIdx - left + 1); // 不关心中位数的值，保证中位数在正确的位置
    int idx = partition(a, left, right, baseIdx), cur = idx - left + 1;
    if(k == cur) return a[idx];
    else if(k < cur) return bfprt(a, left, idx - 1, k);
    else return bfprt(a, idx + 1, right, k - cur);
}

动态规划

基本步骤

找出最优解的性质，并刻划其结构特征。
递归地定义最优值。
以自底向上的方式计算出最优值。
根据计算最优值时得到的信息，构造最优解。

矩阵连乘

public static void matrixChain(int[] p, int[][] m, int[][] s) {
    int n = p.length - 1;
    for (int i = 1; i <= n; i++) m[i][i] = 0;
    for (int r = 2; r <= n; r++)
        for (int i = 1; i <= n - r + 1; i++) {
            int j = i + r - 1;
            m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
            s[i][j] = i;
            for (int k = i + 1; k < j; k++) {
                int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (t < m[i][j]) {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
}

最优子结构

当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质。

例如，矩阵连乘计算次序问题的最优解包含着其子问题的最优解，这种性质称为最优子结构性质。

利用问题的最优子结构性质，以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。

重叠子问题

在递归算法自顶向下求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。

动态规划算法，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。

LIS最长单调递增子序列

设序列为 a[0:n-1]，记 b[i]：以 a[i] 为结尾元素的最长递增子序列的长度。

则序列 a 的最长递增子序列长度为：max{b[i]}, 0<=i<n

如何求 b[i] ?

b[0] = 1，b[i] = max{b[k]} + 1, (0<=k<i, a[k]<=a[i])

public static int LIS() {
    for(int i = 1, b[0] = 1; i < n; i++){
        for(int j = 0, k = 0; j < i; j++) {
            if(a[j] <= a[i] && k < b[j]) k = b[j];
        }
        b[i] = k + 1;
    }
}

LCS最长公共子序列

给定 2 个序列，\(X={x_1,x_2,…,x_m}\) 和 \(Y={y_1,y_2,…,y_n}\)，找出 X 和 Y 的最长公共子序列。

设序列 \(X={x_1,x_2,…,x_m}\) 和 \(Y={y_1,y_2,…,y_n}\) 的最长公共子序列为 \(Z={z_1,z_2,…,z_k}\)，则

1)若 \(x_m=y_n\)，则 \(z_k=x_m=y_n\)，且 \(Z_{k-1}\) 是 \(X_{m-1}\) 和 \(Y_{n-1}\) 的最长公共子序列。

2)若 \(x_m≠y_n\)，则 \(Z\) 是 \(X_{m-1}\) 和 \(Y\) 的最长公共子序列，\(X\) 和 \(Y_{n-1}\) 的最长公共子序列，中较长的序列。

2 个序列的最长公共子序列包含了这 2 个序列的前缀的最长公共子序列。因此，最长公共子序列问题具有最优子结构性质。

由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用 \(c[i][j]\) 记录序列的最长公共子序列的长度。其中，\(X_i={x_1,x_2,…,x_i}\)；\(Y_j={y_1,y_2,…,y_j}\)。当 \(i=0\) 或 \(j=0\) 时，空序列是 \(X_i\) 和 \(Y_j\) 的最长公共子序列。故此时 \(c[i][j]=0\)。其他情况下，由最优子结构性质可建立递归关系如下：

i=0,j=0：c[i][j]=0
i,j>0; x[i]==y[i]：c[i][j]=c[i-1][j-1]+1
i,j>0; x[i]!=y[i]：c[i][j]=max{c[i][j-1],c[i-1][j]}

memset(dp, 0, sizeof(dp));
for (int i = 0; i < strlen(a); ++i) {
    for (int j = 0; j < strlen(b); ++j) {
        if(a[i] == b[j]) dp[i+1][j+1] = dp[i][j] + 1;
        else dp[i+1][j+1] = max(dp[i+1][j], dp[i][j+1]);
    }
}

Algorithm lcsLength(x, y){
    m = x.length - 1;
    n = y.length - 1;
    c[i][0] = 0; c[0][i] = 0;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            if (x[i] == y[j]) {
                c[i][j] = c[i-1][j-1] + 1;
            }else if (c[i-1][j] >= c[i][j-1]) {
                c[i][j] = c[i-1][j];
            }else{
                c[i][j] = c[i][j-1];
            }
}

Algorithm lcs(int i, int j, char [] x){
    if (i == 0 || j == 0) return;
    if (x[i] == y[i]){
        lcs(i-1, j-1, x);
        print(x[i]);
    }else if (c[i-1][j] >= c[i][j-1]) lcs(i-1, j, x);
    else lcs(i, j-1, x);
}

分治法与动态规划的区别

分治法与动态规划有何共同点？提示：从所适用问题的特点，解决问题的方式上阐述
- 两者所解决的问题，都能划分为若干个规模较小的子问题
- 这些子问题具有最优子结构性质
- 能通过子问题的最优解自底向上地得到问题的最优解
分治法与动态规划又有何不同？提示：从子问题的角度阐述
- 分治法适用于子问题相互独立的情况，即子问题之间不存在公共子问题
- 动态规划适用于子问题存在重叠的情况，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果

贪心算法

基本思想

贪心算法总是做出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

活动安排问题

/*
 * 各活动的起始时间和结束时间存储于数组s和f中且按结束时间的非减序排列
 * a数组记录是否安排相应活动
 */
public static int greedySelector(int [] s, int [] f, boolean a[]){
    int n = s.length-1;
    a[1] = true;
    int j = 1;
    int count = 1;
    for (int i = 2; i <= n; i++) {
        if (s[i] >= f[j]) {
            a[i] = true;
            j = i;
            count++;
        }else a[i] = false;
    }
    return count;
}

最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

贪心选择性质

所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

在动态规划算法中，每步所做出的选择往往依赖于相关子问题的解。因而只有在解出相关子问题后，才能做出选择。而在贪心算法中，仅在当前状态下做出最好选择，即局部最优选择。然后再去解做出这个选择后产生的相应的子问题。

贪心算法和动态规划算法都要求问题具有最优子结构性质，这是两类算法的一个共同点。

对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。（即证明有解必有贪心解）

贪心算法求解背包问题

基本步骤：

首先计算每种物品单位重量的价值 \(V_i/W_i\)
然后，依贪心选择策略，将尽可能多的单位重量价值最高的物品装入背包
若将这种物品全部装入背包后，背包内的物品总重量未超过 C，则选择单位重量价值次高的物品并尽可能多地装入背包。
依此策略一直地进行下去，直到背包装满为止。

public static float knapsack(float c, float[] w, float[] v,float[] x){
    int n = v.length;
    Element [] d = new Element [n];
    for (int i = 0; i < n; i++) d[i] = new Element(w[i], v[i], i);
    MergeSort.mergeSort(d);
    int i;
    float opt = 0;
    for (i = 0; i < n; i++) x[i] = 0;
    for (i = 0; i < n; i++) {
        if (d[i].w > c) break;
        x[d[i].i] = 1;
        opt += d[i].v;
        c -= d[i].w;
    }
    if (i < n){
        x[d[i].i] = c / d[i].w;
        opt += x[d[i].i] * d[i].v;
    }
    return opt;
}

对于 0-1 背包问题，贪心选择之所以不能得到最优解是因为在这种情况下，它无法保证最终能将背包装满，部分闲置的背包空间使每公斤背包空间的价值降低了。

事实上，在考虑 0-1 背包问题时，应比较选择该物品和不选择该物品所导致的最终方案，然后再作出最好选择。

最优装载问题

public static float loading(float c, float[] w, int[] x){
    int n = w.length;
    Element [] d = new Element [n];
    for (int i = 0; i < n; i++) d[i] = new Element(w[i], i);
    MergeSort.mergeSort(d);
    float opt = 0;
    for (int i = 0; i < n; i++) x[i] = 0;
    for (int i = 0; i < n && d[i].w <= c; i++) {
        x[d[i].i] = 1;
        opt += d[i].w;
        c -= d[i].w;
    }
    return opt;
}

哈夫曼编码

应用

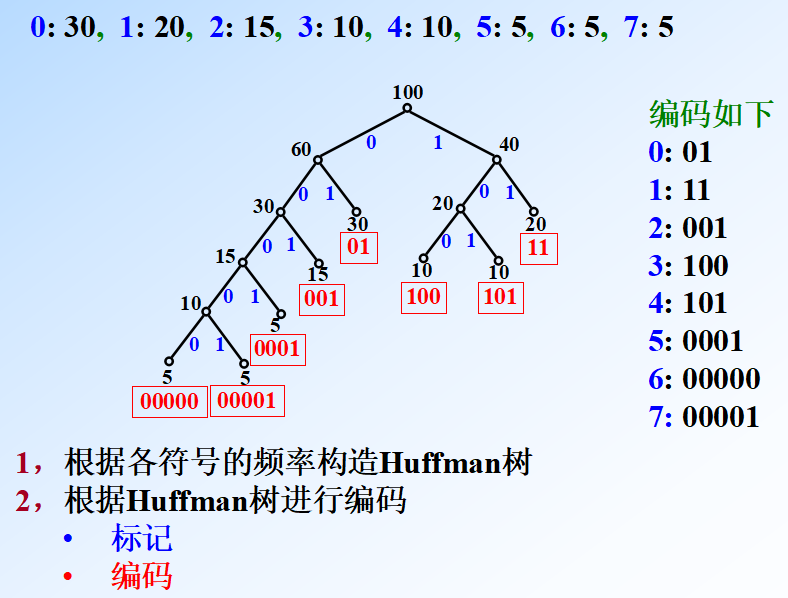
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。给出现频率高的字符较短的编码，出现频率较低的字符以较长的编码，可以大大缩短总码长。

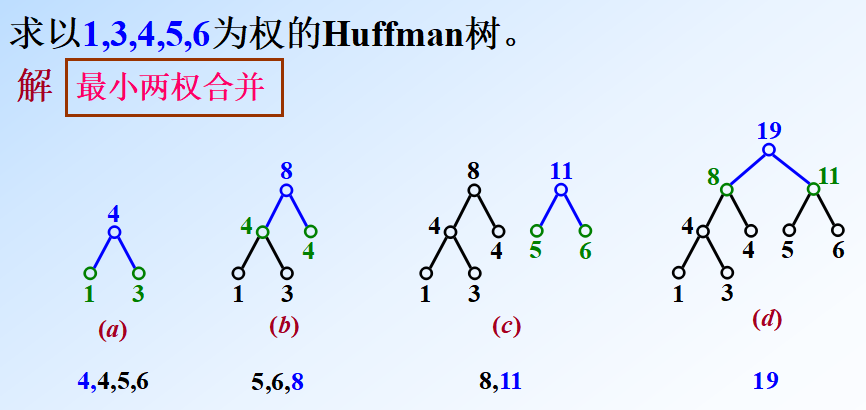
构造哈夫曼编码

哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树 T。
算法以 C 个叶结点开始，执行 C-1 次的“合并”运算后产生最终所要求的树 T。

huffman-1

huffman-2

单源最短路径

单源最短路问题

给定带权有向图 G=(V,E)，其中每条边的权是非负实数。另外，还给定 V 中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。

Dijkstra 算法

Dijkstra 算法是解单源最短路径问题的贪心算法。其基本思想是，设置顶点集合 S 并不断地作贪心选择来扩充这个集合。一个顶点属于集合 S 当且仅当从源到该顶点的最短路径长度已知。

基本步骤：

初始时，S 中仅含有源。
设 u 是 G 的某一个顶点，把从源到 u 且中间只经过 S 中顶点的路称为从源到 u 的特殊路径，并用数组 dist 记录当前每个顶点所对应的最短特殊路径长度。
Dijkstra 算法每次从 V-S 中取出具有最短特殊路长度的顶点 u，将 u 添加到 S 中，同时对数组 dist 作必要的修改。
一旦 S 包含了所有 V 中顶点，dist 就记录了从源到所有其他顶点之间的最短路径长度。

int cost[MAX_V][MAX_V];  // cost[u][v]表示边e=(u,v)的权值（不存在这条边时设为INF）
int dist[MAX_V];  // 顶点s出发的最短距离
bool used[MAX_V];  // 已经使用过的图
int V;  // 顶点数

// 求从起点s出发到各个顶点的最短距离
void dijkstra(int s){
    fill(dist, dist + V, INF);
    fill(used, used + V, false);
    dist[s] = 0;
    while(true){
        int v = -1;
        // 从尚未使用过的顶点中选择一个距离最小的顶点
        for(int u = 0; u < V; u++){
            if(!used[u] && (v == -1 || dist[u] < dist[v])) v = u;
        }
        if(v == -1) break;
        used[v] = true;
        for(int u = 0; u < V; u++){
            dist[u] = min(dist[u], dist[v] + cost[v][u]);
        }
    }
}

最小生成树

定义

设 \(G =(V,E)\) 是无向连通带权图，即一个网络。\(E\) 中每条边 \((v,w)\) 的权为 \(c[v][w]\)。如果 \(G\) 的子图 \(G’\) 是一棵包含 \(G\) 的所有顶点的树，则称 \(G’\) 为 \(G\) 的生成树。生成树上各边权的总和称为该生成树的耗费。在 \(G\) 的所有生成树中，耗费最小的生成树称为 \(G\) 的最小生成树。

最小生成树性质

设 \(G=(V,E)\) 是连通带权图，\(U\) 是 \(V\) 的真子集。如果 \((u,v) \in E\)，且 \(u \in U\)，\(v \in V-U\)，且在所有这样的边中，\((u,v)\) 的权 \(c[u][v]\) 最小，那么一定存在 \(G\) 的一棵最小生成树，它以 \((u,v)\) 为其中一条边。这个性质有时也称为 MST 性质。

Prim算法

设 \(G=(V,E)\) 是连通带权图，\(V={1,2,…,n}\)。构造 \(G\) 的最小生成树的 Prim 算法的基本思想是：

首先置 \(S=\{1\}\)，
然后，只要 \(S\) 是 \(V\) 的真子集，就作如下的贪心选择
选取满足条件 \(i \in S\)，\(j \in V-S\)，且 \(c[i][j]\) 最小的边，将顶点j添加到 \(S\) 中。
这个过程一直进行到 \(S=V\) 时为止。在这个过程中选取到的所有边恰好构成 G 的一棵最小生成树。

int cost[MAX_V][MAX_V];  // cost[u][v]表示边e=(u,v)的权值（不存在这条边时设为INF）
int mistcost[MAX_V];  // 从集合X出发的边到每个顶点的最小权值
bool used[MAX_V];  // 顶点i是否包含在集合X中
int V;  // 顶点数

int prim(){
    for(int i = 0; i < V; i++){
        mincost[i] = INF;
        used[i] = false;
    }
    mincost[0] = 0;
    int res = 0;
    while(true) {
        int v = -1;
        // 从不属于X的顶点中选取从X到其权值最小的顶点
        for(int u = 0; u < V; u++){
            if(!used[u] && (v == -1 || mincost[u] < mincost[v])) v = u;
        }
        if(v == -1) break;
        used[v] = true;  // 把顶点v加入X
        res += mincost[v];  // 把边的长度加到结果里
        for(int u = 0; u < V; u++){
            mincost[u] = min(mincost[u], cost[v][u]);
        }
    }
    return res;
}

Kruskal 算法

Kruskal 算法构造 \(G\) 的最小生成树的基本思想是：

首先将 \(G\) 的 \(n\) 个顶点看成 \(n\) 个孤立的连通分支。
将所有的边按权从小到大排序。
然后从第一条边开始，依边权递增的顺序查看每一条边，并按下述方法连接 2 个不同的连通分支
当查看到第 \(k\) 条边 \((v,w)\) 时，如果端点 \(v\) 和 \(w\) 分别是当前 2 个不同的连通分支 \(T1\) 和 \(T2\) 中的顶点时，就用边 \((v,w)\) 将 \(T1\) 和 \(T2\) 连接成一个连通分支，然后继续查看第 \(k+1\) 条边；
如果端点 \(v\) 和 \(w\) 在当前的同一个连通分支中，就直接再查看第 \(k+1\) 条边。
这个过程一直进行到只剩下一个连通分支时为止。

struct edge {
    int u;
    int v;
    int cost;
};

bool cmp(const edge &e1, const edge &e2) {
    return e1.cost < e2.cost;
}

edge es[MAX_E];
int V, E;  // 顶点数和边数

int krustral() {
    sort(es, es + E, comp);  // 按照edge.cost的顺序从小到大排列
    init_union_find(V);  // 并查集初始化
    int res = 0;
    for(int i = 0; i < E; i++){
        edge e = es[i];
        if(!same(e.u, e.v)){
            unite(e.u, e.v);
            res += e.cost;
        }
    }
    return res;
}

并查集

主要操作

初始化集合中每个元素单独作为一个子集。
查找查找元素 x 所在的子集序号。常用来判断元素 x 和 y 是否在同一子集中。
合并将元素 x 和 y 分别所在的子集合并为一个子集。

算法实现

// 用编号代表每个元素，数组par表示父亲的编号，当par[x]=x时，x是所在树的树根
int par[MAX_N];  // 父亲
int rank[MAX_N];  // 树的高度

// 初始化n个元素
void init(int n) {
    for(int i = 0; i < n; i++) {
        par[i] = i;
        rank[i] = 0;
    }
}

// 查询树的根
int find(int x) {
    if(par[x] == x) {
        return x;
    } else {
        return par[x] = find(par[x]);
    }
}

// 合并x和y所属的集合
void unite(int x, int y) {
    x = find(x);
    y = find(y);
    if(x == y) return;
    if(rank[x] < rank[y]) {
        par[x] = y;
    } else {
        par[y] = x;
        if(rank[x] == rank[y]) rank[x]++;
    }
}

优先队列

主要操作

初始化将给定多个元素初始化为优先队列。
出队将优先权最大的元素x出队，并调整结构为优先队列。
入队加入元素x，并调整结构为优先队列。

算法实现

// 节点从0开始编号
int heap[MAX_N], sz = 0;
void push(int x) {
    // 自己节点的编号
    int i = sz++;
    while(i > 0) {
        // 父亲节点的编号
        int p = (i-1) / 2;
        // 如果已经没有大小颠倒则退出
        if(heap[p] <= x) break;
        // 把父亲节点的数组放下来，而把自己提上去
        heap[i] = heap[p];
        i = p;
    }
    heap[i] = x;
}

int pop() {
    // 最小值
    int ret = heap[0];
    // 要提到根的数值
    int x = heap[--sz];
    // 从根开始向下交换
    int i = 0;
    while(i * 2 + 1 < sz) {
        // 比较儿子的值
        int a = i * 2 + 1, b = i * 2 + 2;
        if(b < sz && heap[b] < heap[a]) a = b;
        // 如果已经没有大小颠倒则退出
        if(heap[a] >= x) break;
        // 把儿子的数值提上来
        heap[i] = heap[a];
        i = a;
    }
    heap[i] = x;
    return ret;
}

回溯法

定义

为了避免生成那些不可能产生最佳解的问题状态，要不断地利用限界函数(bounding function)来处死那些实际上不可能产生所需解的活结点，以减少问题的计算量。具有限界函数的深度优先生成法称为回溯法。

基本思想

针对所给问题，定义问题的解空间；
确定易于搜索的解空间结构；
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

常用剪枝函数：用约束函数在扩展结点处剪去不满足约束的子树；用限界函数剪去得不到最优解的子树。 这种方法适用于解一些组合数相当大的问题。

回溯法的特征

用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻，算法只保存从根结点到当前扩展结点的路径。如果解空间树中从根结点到叶结点的最长路径的长度为 \(h(n)\)，则回溯法所需的计算空间通常为 \(O(h(n))\)。

递归回溯

void backtrack(int t) {
    if (t > n) output(x);
    else
        for (int i = f(n,t); i <= g(n,t); i++) {
            x[t] = h(i);
            if (constraint(t) && bound(t)) backtrack(t + 1);
        }
}

迭代回溯

void iterativeBacktrack() {
    int t = 1;
    while (t > 0) {
        if (f(n,t) <= g(n,t))
            for (int i = f(n,t); i <= g(n,t); i++) {
                x[t] = h(i);
                if (constraint(t) && bound(t)) {
                    if (solution(t)) output(x);
                    else t++;
                }
            }
        else t--;
    }
}

求S的所有元素个数小于4的子集

已知集合 \(S=\{a,b,c,d,e,f,g\}\)，请编程输出 \(S\) 的所有元素个数小于 4 的子集。

#define n 7
char s[n] = {a,b,c,d,e,f,g};
int x[n+1];
void output(int* x) {
}
void all_subset() {
    backtrack(0);
}
void backtrack (int t) {
    if (t >= n) output(x);
    else
        for (int i = 0; i <= 1; i++) {
            x[t] = i;
            if(count(x, t) < 4) backtrack(t + 1);
        }
}

求S的所有元素和小于8的子集

已知集合 \(S=\{1,2,3,4,5,6,7\}\)，请编程输出 \(S\) 的所有元素和小于 8 的子集。

#define n 7
char s[n] = {1,2,3,4,5,6,7};
int x[n+1];
void output(int* x) {
}
void all_subset() {
    backtrack(0);
}
void backtrack (int t) {
    if (t >= n) output(x);
    else
        for (int i = 0; i <= 1; i++) {
            x[t] = i;
            if(sum(x, t) < 8) backtrack(t + 1);
        }
}

求S满足元素奇偶性相同且和小于8的子集

已知集合 \(S=\{1,2,3,4,5,6,7\}\)，请编程输出 \(S\) 的所有满足下列条件的子集：元素奇偶性相同，且和小于 8。

#define n 7
char s[n] = {1,2,3,4,5,6,7};
int x[n+1];
void output(int* x) {
}
void all_subset() {
    backtrack(0, 0, -1);
}
void backtrack (int t, int sum, int prior) {
    if (t >= n) output(x);
    else {
        x[t] = 0, backtrack(t + 1, sum, prior);
        x[t] = 1;
        sum += s[t];
        if(sum < 8 && (prior == -1 || (s[t] - s[prior]) % 2 == 0) {
            backtrack(t + 1, sum, t);
        }
    }
}

求S的所有排列

已知集合 \(S=\{1,2,3,4,5,6,7\}\)，请编程输出 S 的所有排列。

#define n 7
char s[n+1] = {1,2,3,4,5,6,7};
void output(char* s) {
}
void all_permutation() {
    backtrack(0);
}
void backtrack (int t) {
    if (t >= n) output(s);
    else
        for (int i = t; i < n; i++) {
            swap(s[t], s[i]);
            backtrack(t + 1);
            swap(s[t], s[i]);
        }
}

求S的所有满足奇偶数相间出现的排列

已知集合 \(S=\{1,2,3,4,5,6,7,8\}\)，请编程输出 S 的所有满足下列条件的排列：奇偶数相间出现。

#define n 7
char s[n+1] = {1,2,3,4,5,6,7};
void output(char* s) {
}
void all_permutation() {
    backtrack(0);
}
void backtrack (int t) {
    if (t >= n) output(s);
    else
        for (int i = t; i < n; i++) {
            swap(s[t], s[i]);
            if(legal(t)) backtrack(t + 1);
            swap(s[t], s[i]);
        }
}
bool legal(int t){
    bool bRet = true;
    if(t > 0) bRet &&= ((s[t - 1] - s[t]) % 2 == 1);
    return bRet;
}

0-1 背包问题

重量 \(w=\{2,2,3,4,5,5,6\}\)，价值 \(v=\{3,4,3,4,5,8,7\}\)，\(C=16\)，求背包的最大价值。

#define n 7
int C = 16;
int w[n] = {2,2,3,4,5,5,6};
int v[n] = {3,4,3,4,5,8,7};
int x[n+1], Max = 0;
void output(int* x);
void main() {
    backtrack(0);
}
void backtrack (int t) {
    if (t >= n) process(x);
    else
        for (int i = 0; i <= 1; i++) {
            x[t] = i;
            if(legal(t)) backtrack(t + 1);
        }
}
bool legal(int t){
    int sum = 0;
    for(int i = 0; i <= t; i++){
        sum += x[i] * w[i];
    }
    return sum <= C;
}
void process(x) {
    for(int i = 0; i < n; i++){
        sum += x[i] * v[i];
    }
    if(Max < sum) Max = sum;
}

装载问题

void backtrack (int i) {  // 搜索第i层结点
    if (i > n) {  //到达叶结点更新最优解bestx
        return;
    }
    r -= w[i];
    if (cw + w[i] <= c) {  // 搜索左子树
        x[i] = 1;
        cw += w[i];
        backtrack(i + 1);
        cw -= w[i];
    }
    if (cw + r > bestw)  {  // 搜索右子树
        x[i] = 0;
        backtrack(i + 1);
    }
    r += w[i];
}

n皇后问题

boolean place(int k) {
    for (int j = 1; j < k; j++)
        if (abs(k - j) == abs(x[j] - x[k])) return false;
    return true;
}
void backtrack(int t) {
    if (t > n) output(x);
    else
        for (int i = t; i <= n; i++) {
            swap(x[t], x[i]);
            if (place(t)) backtrack(t + 1);
            swap(x[t], x[i]);
        }
}