多边形游戏

发表于 更新于 分类于 阅读次数： 本文字数： 1.9k 阅读时长 ≈ 7 分钟

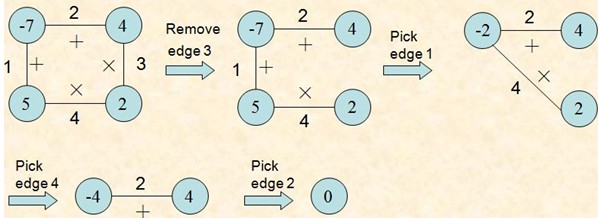
polygon-game

项目要求实现给出得到最高分的删除方案且界面友好。

多边形游戏

游戏简介

多边形游戏是一个单人玩的游戏，开始时有一个由 n 个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符 + 或 *。所有边依次用整数从 1 到 n 编号，游戏第 1 步，将一条边删除。

随后 n-1 步按以下方式操作：

  1. 选择一条边 E 以及由 E 连接着的两个顶点 \(V_1\) 和 \(V_2\);

  2. 用一个新的顶点取代边E以及由E连接着的两个顶点 \(V_1\) 和 \(V_2\)。将由顶点 \(V_1\) 和 \(V_2\) 的整数值通过边E上的运算得到的结果赋予新顶点。

最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值。

问题：对于给定的多边形，计算最高分。

算法设计

最优子结构性质

设所给的多边形的顶点和边的顺时针序列为

\[ op[1], v[1], op[2], v[2], ..., op[n], v[n] \]

其中，\(op[i]\) 表示第 \(i\) 条边所对应的运算符，\(v[i]\) 表示第 \(i\) 个顶点上的数组，\(i=1\sim n\)。

在所给多边形中，从顶点 \(i(1 \leq i \leq n)\) 开始，长度为 \(j\) (链中有 \(j\) )个顶点的顺时针链 \(p(i+s)\) 可表示为

\[ v[i], op[i+1], ..., v[i+j-1] \]

如果这条链的最后一次合并运算在 \(op[i+s]\) 处发生 \((1 \leq s \leq j-1)\)，则可以在 \(op[i+s]\) 处将链分割为两个子链 \(p(i,s)\) 和 \(p(i+s,j-s)\)。

设 \(m_1\) 是对子链 \(p(i,s)\) 的任意一种合并方式得到的值，而 \(a\) 和 \(b\) 分别是在所有可能的合并中得到的最小值和最大值。\(m_2\) 是 \(p(i+s,j-s)\) 的任意一种合并方式得到的值，而 \(c\) 和 \(d\) 分别是在所有可能的合并中得到的最小值和最大值。依此定义有

\[ a \leq m_1 \leq b,\; c \leq m_2 \leq d \]

由于子链 \(p(i,s)\) 和 \(p(i+s,j-s)\) 的合并方式决定了 \(p(i,j)\) 在 \(op[i+s]\) 处断开后的合并方式，在 \(op[i+s]\) 处合并后其值为

\[ m =(m_1)op[i+s](m_2) \]

  • 当 \(op[i+s]='+'\) 时，显然有

    \[ a+c \leq m \leq b+d \]

  • 当 \(op[i+s]='*'\) 时，由于 \(v[i]\) 可取负整数，子链的最大值相乘未必能得到主链的最大值。但最大值一定是在边界点达到，即

    \[ min \left\{ ac,ad, bc,bd \right\} \leq m \leq max \left\{ ac,ad,bc,bd\right\} \]

    换句话说，主链的最大值和最小值可由子链的最大值和最小值得到。例如，当 \(m=ac\) 时，最大主链由它的两条最小链组成；同理当 \(m=bd\) 时，最大主链由它的两条最大子链组成。

递归求解

为了求链合并的最大值，必须同时求子链合并的最大值和最小值。

设 \(m[i,j,0]\) 是链 \(p(i,j)\) 合并的最小值，而 \(m[i,j,1]\) 是最大值。若最优合并在 \(op[i+s]\) 处将 \(p(i,j)\) 分成两个长度小于 \(j\) 的子链 \(p(i,i+s)\) 和 \(p(i+s,j-s)\)，且从顶点 \(i\) 开始的长度小于 \(j\) 的子链的最大值和最小值均已计算出。记

\[ a=m[i,i+s,0]\\ b=m[i,i+s,1]\\ c =m[i+s,j-s,0]\\ d=m[i+s,j-s,1] \]

  1. 当 \(op[i+s]='+'​\) 时，

\[ m[i,j,0]=a+c\\ m[i,j,1]=b+d \]

  1. 当 \(op[i+s]='*'\) 时，

\[ m[i,j,0]=min\left\{ac,ad,bc,bd\right\}\\ m[i,j,1]=min\left\{ac,ad,bc,bd\right\} \]

综合 (1) 和 (2)，将 \(p(i,j)\) 在 \(op[i+s]\) 处断开的最大值记为 \(maxf(i,j,s)\)，最小值记为 \(minf(i,j,s)\)，则

\[ minf(i,j,s)=\left\{\begin{matrix} a+c \qquad \qquad \qquad \qquad \; op[i+s]='+' \\ min\left\{ ac,ad,bc,bd\right\} \qquad op[i+s]='*' \end{matrix}\right. \]

\[ maxf(i,j,s)=\left\{\begin{matrix} b+d \qquad \qquad \qquad \qquad \; op[i+s]='+' \\ min\left\{ ac,ad,bc,bd\right\} \qquad op[i+s]='*' \end{matrix}\right. \]

由于最优断开位置 \(s\) 有 \(1 \leq s \leq j-1\) 的 j-1 种情况，由此可知

\[ m[i,j,0] = \min_{i \leq s < j }\left\{minf(i,j,s)\right\} \qquad 1 \leq i,j \leq n \\ m[i,j,1] = \max_{i \leq s < j }\left\{maxf(i,j,s)\right\} \qquad 1 \leq i,j \leq n \]

初始边界为

\[ m[i,1,0]=v[i] \qquad 1 \leq i \leq n \\ m[i,1,1]=v[i] \qquad 1 \leq i \leq n \]

\(m[i,n,1]\) 即为游戏首次删去第 \(i\) 条边后得到的最大得分。

算法描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
import java.util.HashMap;
import java.util.Scanner;
import java.util.Stack;

public class PloygonAgent {
    private int n; //多边形边数
    private char[] op; //每条边的对应的操作（从1开始计数）
    private int[] v; //每个顶点数值（从1开始计数）
    private long[][][] m; //m[i][n][1]：代表一开始删除第i条边，长度为n的链（包含n个顶点），所能得到的最大值
                          //m[i][n][0]：代表一开始删除第i条边，长度为n的链，所能得到的最小值
    private int[][][] cut; //记录合并点的数组
    private Stack<Integer> stack; //用栈保存合并边的顺序
    private int firstDelEdge; //记录最优情况下，第1条删除的边
    private long bestScore; //记录最优得分

    public PloygonAgent(int n, long[][][] m, char[] op, int[] v){
        this.n = n;
        this.m = m;
        this.op = op;
        this.v = v;
        this.cut = new int[n+1][n+1][2];
        this.stack = new Stack<>();
    }

    private HashMap<String, Long> minMax(int i, int s, int j, HashMap<String, Long> resMap){
        int r = (i+s-1) % n + 1;
        long a = m[i][s][0], b = m[i][s][1], c = m[r][j-s][0], d = m[r][j-s][1];
        if(op[r] == '+'){
            resMap.put("minf", a+c);
            resMap.put("maxf", b+d);
        }else{
            long[] e = new long[]{0, a*c, a*d, b*c, b*d};
            long minf = e[1], maxf = e[1];
            for (int k = 2; k < 5; k++){
                if(minf > e[k]) minf = e[k];
                if(maxf < e[k]) maxf = e[k];
            }
            resMap.put("minf", minf);
            resMap.put("maxf", maxf);
        }
        return resMap;
    }

    private long polyMax(){
        HashMap<String, Long> resMap = new HashMap<>();
        for (int j = 2; j <= n; j++){ //链的长度
            for(int i = 1; i<= n; i++){ //删除第i条边
                m[i][j][0] = Long.MAX_VALUE;
                m[i][j][1] = Long.MIN_VALUE;
                for(int s = 1; s < j; s++){ //断开的位置
                    resMap = this.minMax(i, s, j, resMap);
                    if(m[i][j][0] > resMap.get("minf")){
                        m[i][j][0] = resMap.get("minf");
                        cut[i][j][0] = s; //记录该链取得最小值的断点
                    }
                    if(m[i][j][1] < resMap.get("maxf")){
                        m[i][j][1] = resMap.get("maxf");
                        cut[i][j][1] = s; //记录该链取得最大值的断点
                    }
                }
            }
        }
        bestScore = m[1][n][1];
        firstDelEdge = 1; //一开始删除的边，初始化为第一条边
        for (int i = 2; i <= n; i++){
            if(bestScore < m[i][n][1]){
                bestScore = m[i][n][1];
                firstDelEdge = i; //如果一开始删除第i边有更优的结果，则更新
            }
        }
        for(int i=1; i<=n; i++){ //一开始删除第i条边所能得到的最大分数
            System.out.println("i=" + i + " " + m[i][n][1]);
        }
        System.out.println("firstDelEdge=" + firstDelEdge);
        getBestSolution(firstDelEdge, n, true);
        while (!stack.empty()){ //打印在删除第firstDelEdge条边后的最优合并顺序
            System.out.println("stack--> " + String.valueOf(stack.pop()));
        }
        return bestScore;
    }

    /**
     * 获取最优的合并序列，存入stack中
     * @param i 表示子链从哪个顶点开始
     * @param j 子链的长度（如j=2，表示链中有两个顶点）
     * @param needMax 是否取链的最大值，如果传入值为false，则取子链的最小值
     */
    private void getBestSolution(int i, int j, boolean needMax){
        int s,r;
        if(j == 1) return; //链中只有一个顶点，直接返回
        if(j == 2){
            s = cut[i][j][1];
            r = (i+s-1) % n + 1;
            stack.push(r);
            return; //只有两个顶点时，没有子链，无须递归
        }
        //链中有两个以上的顶点时，将最优的边入栈
        s = needMax ? cut[i][j][1] : cut[i][j][0];
        r = (i+s-1) % n + 1;
        stack.push(r);
        if(this.op[r] == '+'){ //当合并计算为"+"操作时
            if(needMax){ //如果合并得到的父链需要取得最大值
                getBestSolution(i, s, true);
                getBestSolution(r, j-s, true);
            }else { //如果合并得到的父链需要取得最小值
                getBestSolution(i, s, false);
                getBestSolution(r, j-s, false);
            }
        }else{ //当合并计算为"*"操作时
            long a = m[i][s][0], b = m[i][s][1], c = m[r][j-s][0], d = m[r][j-s][1];
            long[] e = new long[]{0, a*c, a*d, b*c, b*d};
            long mergeMax = e[1], mergeMin = e[1];
            for(int k=2; k<=4; k++){
                if(e[k] > mergeMax) mergeMax = e[k];
                if(e[k] < mergeMin) mergeMin = e[k];
            }
            long merge = (needMax) ? mergeMax : mergeMin; //判断合并得到的父链是取最大还是取最小
            if(merge == e[1]){ //子链1和子链2都取最小
                getBestSolution(i, s, false);
                getBestSolution(r, j-s, false);
            }else if(merge == e[2]){ //子链1取最小，子链2取最大
                getBestSolution(i, s, false);
                getBestSolution(r, j-s, true);
            }else if(merge == e[3]){ //子链1取最大，子链2取最小
                getBestSolution(i, s, true);
                getBestSolution(r, j-s, false);
            }else { //子链1和子链2都取最大
                getBestSolution(i, s, true);
                getBestSolution(r, j-s, true);
            }
        }
    }

    private void showPolygon(){
        StringBuilder midBuilder = new StringBuilder();
        StringBuilder botBuilder = new StringBuilder();
        for(int i=1; i<v.length-1; i++){
            midBuilder.append("|").append(String.valueOf(v[i])).append("|");
            midBuilder.append("--").append(op[i + 1]).append("--");
        }
        midBuilder.append("|").append(String.valueOf(v[v.length - 1])).append("|");
        botBuilder.append(" ");
        for (int i=1; i<midBuilder.length()-1; i++){
            if(i == 1 || i == midBuilder.length()-2) botBuilder.append("|");
            else if(i == (midBuilder.length()-1) / 2) botBuilder.append(op[1]);
            else botBuilder.append("_");
        }
        System.out.println(midBuilder.toString());
        System.out.println(botBuilder.toString());

    }

    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        while(scanner.hasNext()){
            int n = scanner.nextInt();
            long[][][] m = new long[n+1][n+1][2];
            char[] op = new char[n+1];
            int[] v = new int[n+1];
            for(int i=1; i<=n; i++){
                op[i] = scanner.next().charAt(0);
                v[i] = scanner.nextInt();
            }
            PloygonAgent ploygonAgent = new PloygonAgent(n, m, op, v);
            ploygonAgent.showPolygon();
            for (int i=1; i<=n; i++){
                m[i][1][0] = m[i][1][1] = v[i];
            }
            long result = ploygonAgent.polyMax();
            System.out.println("BestScore=" + result);
        }
    }
}

最优合并顺序

在上述算法中，为了能简单地得到一个最优的合并顺序，使用了一个 cut[][][] 数组来记录断点位置。

其中只在 m[i][j][0] 或 m[i][j][1] 进行更新时，相应地也进行更新，保证 cut[i][j][0] 为 m[i][j][0] 的最优断点，cut[i][j][1] 为 m[i][j][1] 的最优断点。

这里需要说明的是，cut[i][j][] 中保存的 s，指的是距离顶点 i 的距离，若 s=1，即从说明从 i 顶点开始（包括 i 顶点）只包含一个顶点，也就说要从 i 顶点连着的顺时针的边断开。

其实，计算得到最优分数的过程是一个自底向上的过程，而寻找最优合并顺序则相反，是一个自顶向下的过程。

基本的思路就是，使用一个栈来保存合并边的编号

  • (1)从最后的主链开始，找到最优的合并边，入栈
  • (2)判断合并边的符号，如果是 +，转 (3)；如果是 *，转 (4)
  • (3)如果为 +，判断主链需要最大还是最小
    • 如需最大，则递归取两条子链的最大；
    • 否则，递归取两条子链的最小
  • (4)如果为 *，判断主链需要最大还是最小
    • 如需最大，则在 {ac, ad, bc, bd} 取最大的情况，进行相应递归调用（如 ac，则递归时，两条子链都需要取最小值）
    • 否则，则在 {ac, ad, bc, bd} 取最小的情况，进行相应递归调用

复杂度分析

  • 寻找最优合并顺序

    递归深度最好的情况是 \(logn\)，也就说每次都恰好是对半进行合并；最坏情况是 n-1，每次都合并单个顶点;

    一次递归的过程中，计算时间为常数级别C，所以整个时间复杂度为递归调用次数，即 \(O(C(n-1)) = O(n)\)

  • 总的时间复杂度

    动规过程需要 \(O(n^3)\) 计算时间，加寻找最优合并顺序的时间 \(O(n)\)，总的时间复杂度为 \(O(n^3)\)

测试

这里说明一下 output，前面的 i=x xxx 表示一开始删除那条边所能得到的最高分，接着 firstDelEdge=x 表示一开始删除这条边最终能得到最高分，后面的 stack--> x 是紧接着要按顺序删除的边，最后是该删除方案的得分。

以 Case 1 为例，从左往右对边进行编号，第一条边为 *，连接第一个数字 -5 和最后一个数字 8；类似地，第二条边为 +，连接第一个数字 -5 和第二个数字 -2，其它同理。

  • Case 1

    Input

    1
    2
    5
    * -5 + -2 * -8 * -5 + 8

    Output

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    |-5|--+--|-2|--*--|-8|--*--|-5|--+--|8|
     |_________________*_________________|
    i=1 168
    i=2 480
    i=3 488
    i=4 488
    i=5 120
    firstDelEdge=3
    stack--> 2
    stack--> 1
    stack--> 5
    stack--> 4
    BestScore=488

  • Case 2

    Input

    1
    2
    5
    * -6 + -7 * 0 * 4 + -2

    Ouput

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    |-6|--+--|-7|--*--|0|--*--|4|--+--|-2|
     |________________*_________________|
    i=1 26
    i=2 12
    i=3 26
    i=4 16
    i=5 48
    firstDelEdge=5
    stack--> 3
    stack--> 2
    stack--> 4
    stack--> 1
    BestScore=48

  • Case 3

    Input

    1
    2
    6
    + 5 * 3 + -2 + 1 * -10 * -2

    Ouput

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    |5|--*--|3|--+--|-2|--+--|1|--*--|-10|--*--|-2|
     |_____________________+_____________________|
    i=1 280
    i=2 50
    i=3 130
    i=4 73
    i=5 74
    i=6 63
    firstDelEdge=1
    stack--> 6
    stack--> 4
    stack--> 2
    stack--> 3
    stack--> 5
    BestScore=280

  • Case 4

    Input

    1
    2
    8
    + -2 + 9 * -5 + -4 * -5 * 0 + 7 * -5

    Ouput

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    |-2|--+--|9|--*--|-5|--+--|-4|--*--|-5|--*--|0|--+--|7|--*--|-5|
     |_____________________________+______________________________|
    i=1 2905
    i=2 3969
    i=3 630
    i=4 5080
    i=5 3080
    i=6 3080
    i=7 200
    i=8 3080
    firstDelEdge=4
    stack--> 1
    stack--> 8
    stack--> 7
    stack--> 6
    stack--> 2
    stack--> 3
    stack--> 5
    BestScore=5080

  • Case 5

    Input

    1
    2
    9
    * 0 * -10 + 8 * -4 + 3 * -7 + 7 * -3 * -4

    Ouput

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    |0|--*--|-10|--+--|8|--*--|-4|--+--|3|--*--|-7|--+--|7|--*--|-3|--*--|-4|
     |__________________________________*__________________________________|
    i=1 2816
    i=2 273
    i=3 2000
    i=4 2816
    i=5 5376
    i=6 899
    i=7 19257
    i=8 2758
    i=9 2816
    firstDelEdge=7
    stack--> 4
    stack--> 2
    stack--> 3
    stack--> 1
    stack--> 5
    stack--> 6
    stack--> 9
    stack--> 8
    BestScore=19257

  • Case 6

    Input

    1
    2
    4
    + -7 + 4 * 2 * 5

    Ouput

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    |-7|--+--|4|--*--|2|--*--|5|
     |___________+____________|
    i=1 33
    i=2 33
    i=3 7
    i=4 6
    firstDelEdge=1
    stack--> 4
    stack--> 3
    stack--> 2
    BestScore=33

项目演示和源码

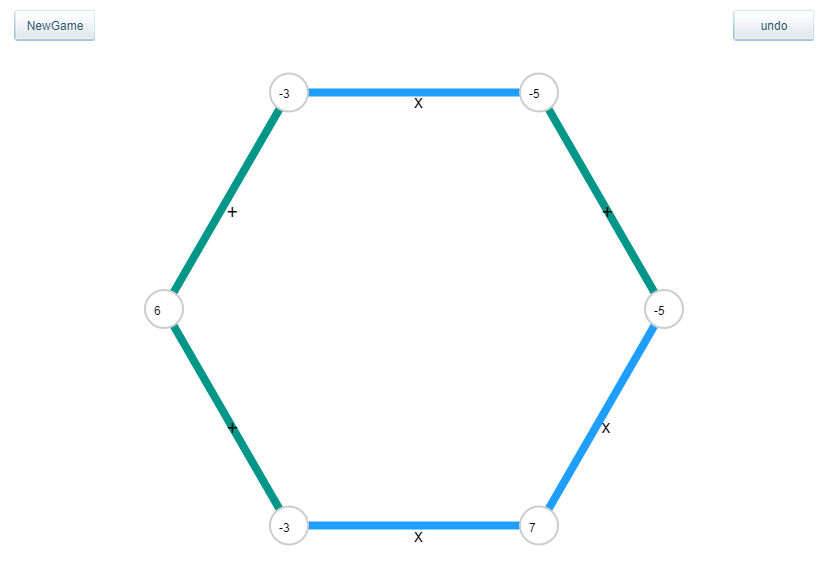
Demo

demo

源码

References

王晓东《算法设计与分析》第三版

https://www.cnblogs.com/Jason-Damon/p/3320565.html