ShellSort

发表于 2019-05-24 更新于 2023-04-08 分类于 algorithm ， sort 阅读次数：本文字数： 679 阅读时长 ≈ 2 分钟

希尔排序（Shellsort），是一种就地比较排序。它可以被看作是交换排序(冒泡排序)或插入排序(插入排序)的泛化。该方法首先对彼此相距很远的元素对进行排序，然后逐步缩小要比较的元素之间的差距。从距离较远的元素开始，它可以比简单的最近邻交换更快地将一些不合适的元素移动到位。1959 年，Donald Shell 出版了第一个版本。Shellsort 的运行时间严重依赖于它使用的间隙序列。对于许多实际的变体，确定它们的时间复杂度仍然是一个悬而未决的问题。

希尔排序（Shellsort）

基本原理

希尔排序，也称 缩小增量排序，是插入排序的一种更高效的改进版本，是 不稳定 的排序算法。

希尔排序是基于插入排序的以下两点性质而提出的改进方法：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

算法步骤

选择增量 gap = length/2，以 gap = gap/2 的方式缩小增量，用序列表示为 {n/2, (n/2)/2, ..., 1}
按增量序列个数 k，对序列进行 k 趟排序
每趟排序，根据对应的增量 gap，将待排序列分割成 gap 个长度子序列，分别对各子序列进行直接插入排序。
当增量 gap 为 1 时，对整个序列进行插入排序。

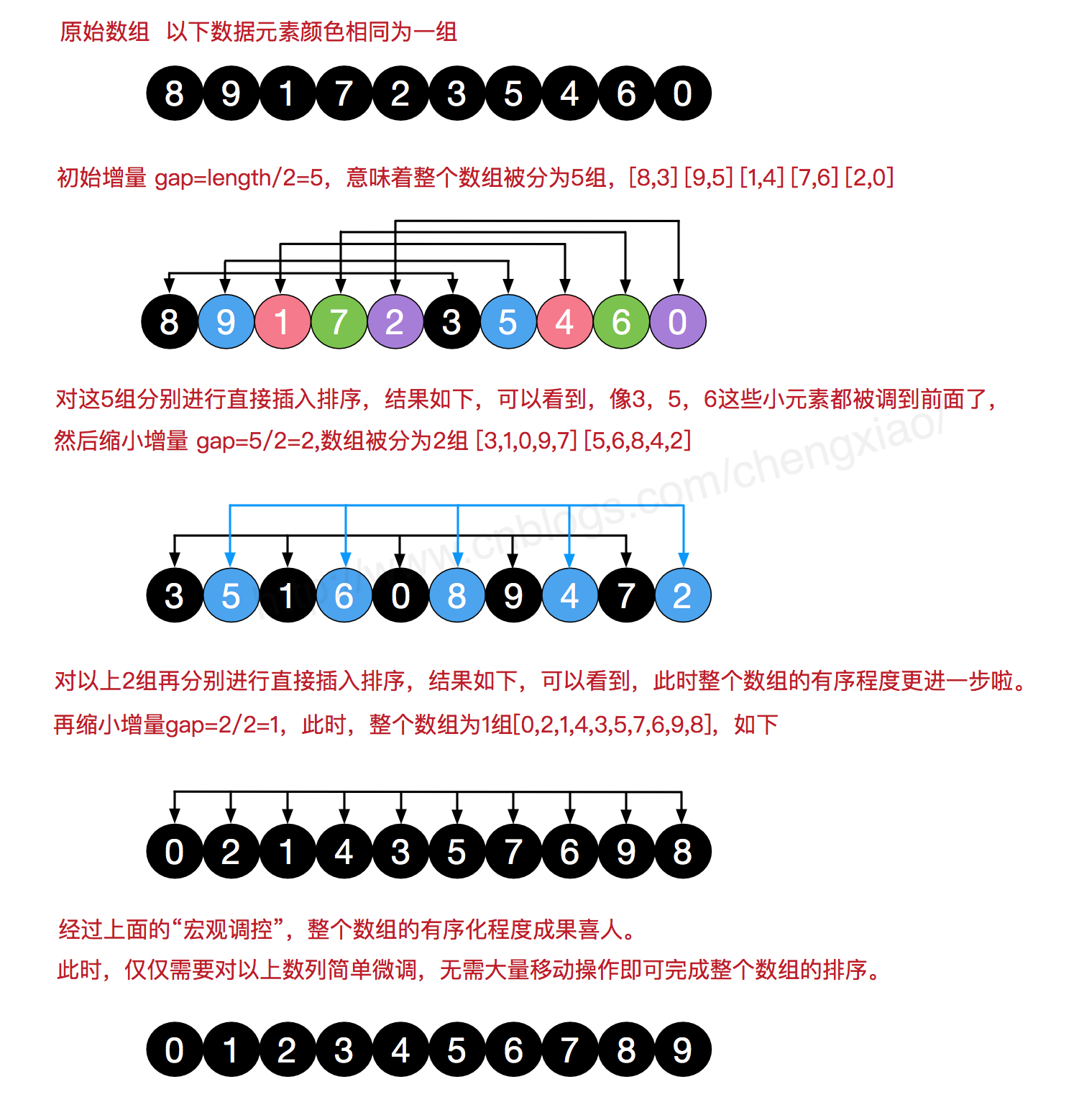
算法图解

图片来源 dreamcatcher-cx 博客图解排序算法(二)之希尔排序

ShellSort

参考实现

import java.util.Arrays;

/**
 * @author wylu
 */
public class ShellSort {

    /**
     * 使用希尔增量序列
     * @param arr 待排序数组
     */
    public static void shellSort(int[] arr) {
        //增量gap，并逐步缩小增量
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            //从第gap个元素开始，逐个对其所在的子序列进行直接插入排序
            for (int i = gap; i < arr.length; i++) {
                int j = i, tmp = arr[i];
                for (; j >= gap && arr[j - gap] > tmp; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = tmp;
            }
        }
    }

    /**
     * 使用Knuth增量序列
     * Knuth增量序列递推式：h(1) = 1, h(i) = 3 * h(i-1) + 1
     * Hibbard增量序列递推式：h(1) = 1, h(i) = 2 * h(i-1) + 1
     * @param arr 待排序数组
     */
    public static void knuthSort(int[] arr) {
        int gap = 1;
        while (gap < arr.length) {
            gap = gap * 3 + 1;
        }

        while (gap > 0) {
            for (int i = gap; i < arr.length; i++) {
                int j = i, tmp = arr[i];
                for (; j >= gap && arr[j - gap] > tmp; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = tmp;
            }
            gap = (gap - 1) / 3;
        }
    }


    public static void main(String[] args) {
        int[] arr = {3, 1, 4, 9, 6, 0, 7, 2, 5, 8};
//        ShellSort.shellSort(arr);
        ShellSort.knuthSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}