应用密码学总结

发表于 更新于 分类于 ， 阅读次数： 本文字数： 4.1k 阅读时长 ≈ 15 分钟

本文主要介绍了应用密码学的相关知识，包括信息安全的三个基本目标、密码学的基本概念、密码算法分类、数论基础、古典密码、安全电子邮件方案、对称密码、单向散列函数、不对称密码、Diffie-Hellman密钥交换和数字签名等方面。其中，介绍了密码学的两个分支：密码编码学和密码分析学，以及密码算法分类的两种方式：按照保密性依赖的基础和按照密钥的特点。此外，还介绍了对称密码算法和非对称密钥算法，以及RSA算法、Euler函数、Euler定理、ElGamal密码体制、Diffie-Hellman密钥交换和数字签名等具体内容。

应用密码学总结

概述

信息安全的三个基本的目标

  • 保密性 Confidentiality 消息能够被安全的传送，即窃听者不能阅读发送的消息。
  • 完整性 Integrity 消息的接收者应该能够验证在传递的过程中消息没有被修改；入侵者不能用假消息代替合法的消息。
  • 可用性 Availability 即保证信息和信息系统随时为授权者提供服务，而不要出现非授权者滥用却对授权者拒绝服务的情况。

数据的安全基于密钥的保密，而不是算法的保密

公钥密码使得无密钥传输的保密通信成为可能

密码学的基本概念

密码学(Cryptology)：研究信息系统安全技术的科学。它包含两个分支：

  • 密码编码学(Cryptography)，对信息进行编码实现隐蔽信息的一门学问
  • 密码分析学(Cryptanalysis)，研究分析破译密码或伪造的学问。 两者相互对立，而又互相促进地向前发展。

密码算法分类-I

按照保密性依赖的基础分为:

  • 受限制的（Restricted)算法: 算法的保密性基于保持算法的秘密。
  • 基于密钥（Key-based)的算法: 算法的保密性基于对密钥的保密。

密码算法分类-II

按照密钥的特点分为：

  • 对称密码算法（Symmetric Cipher)：就是加密密钥和解密密钥相同，或实质上等同，即从一个易于推出另一个。又称秘密密钥算法或单密钥算法。 对称密钥密码又可分为流密码和分组密码
    • 分组密码每次对一块数据(Block)加密例子：DES, IDEA, RC6, Rijndael
    • 流密码每次对一位或一字节加密例子：One-time padding, Vigenére, Vernam
  • 非对称密钥算法（Asymmetric Cipher)：加密密钥和解密密钥不相同，从一个很难推出另一个。又称公钥密钥算法（Public-key Cipher) 。

数论基础

互素

如果a,b的最大公约数为1，则称a,b互素。(注. (a,b)表示a,b的最大公约数) (3,5)=1 a,b互素，a,b不一定是素数，例如(9,4)=1

模运算

模加法

(a + b) mod m = ((a mod m) + (b mod m)) mod m 例: (11 + 15) mod 8 = ((11 mod 8) + (15 mod 8)) mod 8 = (3 + 7) mod 8 = 10 mod 8 = 2

模减法

(a - b) mod m = ((a mod m) - (b mod m)) mod m 例: (15 - 1) mod 7 = ((15 mod 7) - (1 mod 7)) mod 7 = (1 - 1) mod 7 = 0 mod 7 = 0

模乘法

(a × b) mod m = ((a mod m) × (b mod m)) mod m 例: (7 × 9) mod 8 = ((7 mod 8) × (9 mod 8)) mod 8 = (7 × 1) mod 8 = 7 mod 8 = 7

逆元

加法逆元

x的加法逆元y是满足x + y ≡ 0 mod m的数 例: 2 + 6 ≡ 0 mod 8, 6和2互为模8的加法逆元

乘法逆元

x的乘法逆元y是满足x × y ≡ 1 mod m 数。 例：2 × 4 ≡ 1 mod 7，2和4互为模7的乘法逆元

如果m是一个素数，则对每一个0<x<m, 都存在乘法逆元

例： 1 × 1 ≡1 mod 7 2 × 4 ≡1 mod 7 3 × 5 ≡1 mod 7 4 × 2 ≡1 mod 7 5 × 3 ≡1 mod 7 6 × 6 ≡1 mod 7 ​ …

一个定理

1
2
3
4
5
6
7
8
设a, b, c是任意三个不全为零的整数,且
                     a= bq + r                      (1)
其中q是整数, 则(a, b)=(b, r).
对(1)进一步地约束，令b>0,将a除以b所得的商记为q, 余数为r , 则(1)成为
                     a= bq + r, 0<=r<b              (2)
r是a对模b的非负最小剩余。
进一步 (a, b)=(|a|, |b|)=(b, a)
由此我们得到求(a, b)的Euclid辗转相除法

Euclid

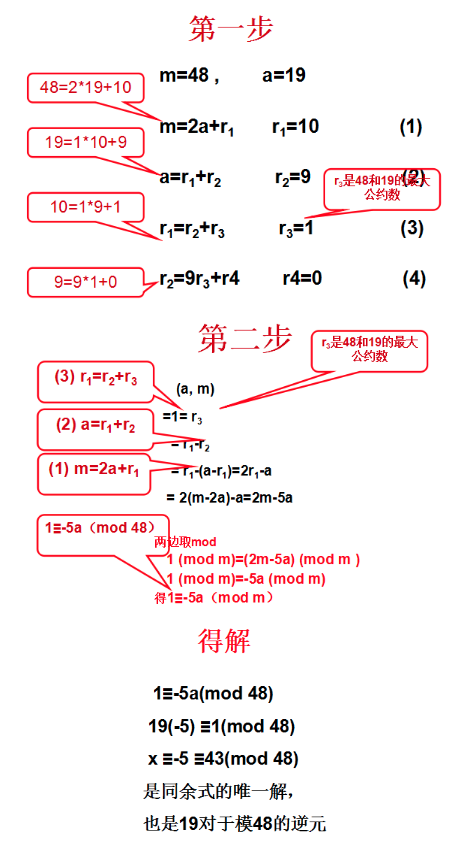
解一次同余式

1
2
3
4
5
6
一个定理:
若 (a, m) = 1, 则一次同余式
                 ax ≡ b (mod m)
有唯一解
例：19x ≡ 1(mod 48)
因为(19, 48) = 1, 所以一次同余式有唯一解，即19对于模48的有唯一逆元。

Solve a congruence

古典密码

单表密码体制

如果明文中不同的位置的同一明文字母在密文中对应的密文字母相同,则称其为单表密码体制。

  • 乘法密码算法

Multiplication cryptographic algorithm

  • 仿射密码算法

Affine cryptographic algorithm

  • 语言的统计特性：频率特征；连接特征；重复特征

多表密码体制

如果明文中不同的位置的同一明文字母在密文中对应的密文字母不同,则称其为多表密码体制。

安全电子邮件方案

PGP产生的背景

你的电子邮件不安全，电子邮件在传输中使用的SMTP协议。

  • 无法保证邮件在传输过程中不被人偷看。
  • 无法确认来源。
  • 无法确定邮件是否在传输过程中被篡改
  • 当邮件被发到错误地址，可能造成信息泄露

PGP提供了一个安全电子邮件解决方案

PGP (Pretty Good Privacy) 具有以下的功能

  • 消息加密
  • 数字签名
  • 完整性确认
  • 数据压缩

PGP加密流程

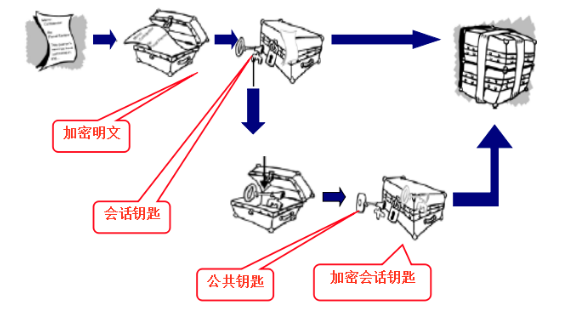
PGP encrypt

PGP解密流程

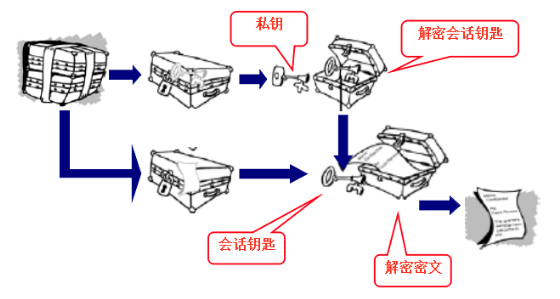
PGP decrypt

PGP整合了对称加密和公钥加密的方案

  • 保持了对称加密算法速度快的特点
  • 具有公钥算法密钥分配方便的特点

PGP数字签名和Hash函数

直接对明文进行数字签名一些问题

  • 速度非常慢
  • 生成大量的数据

PGP的解决方案

  • 对明文使用一种Hash函数, 产生定长的数据, 称为消息摘要
  • PGP使用签名算法对摘要签名
  • PGP将签名和明文一同传输

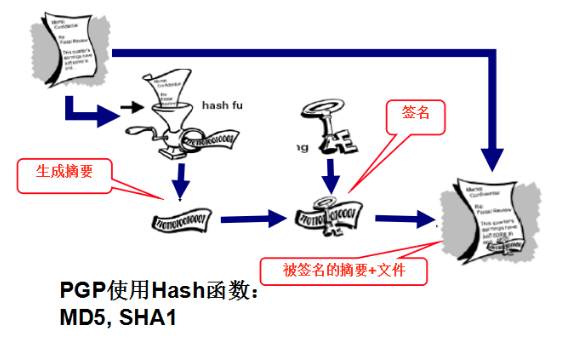
PGP digital signature

公共密钥分发和证明模型

金字塔模型

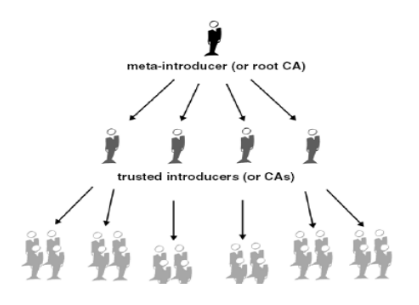
pyramid model

直接信任模型

direct trust model

信任网络

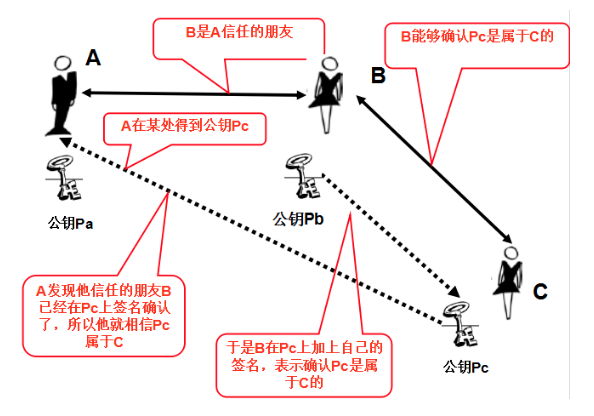
trust network

对称密码

AES的若干要求和评估准则

  • AES的基本要求：比DES快而且比DES安全，分组长度为128比特，密钥长度为128／192（超56比特）。
  • 安全性评估：算法输出的随机性好，抗密码分析能力强，并且有可靠的数学基础。
  • 成本估计准则：许可成本低，在各种平台上的计算高效率和较小的内存空间需求。
  • 算法和实现特性准则：灵活性、硬件和软件适用性、算法的简明性。

具体体现为：

  • 算法处理的密钥和分组长度必须具备灵活的支持范围；
  • 算法在许多不同类型的环境下能够安全和有效地实现；
  • 可以作为序列密码、哈希算法实现；
  • 算法必须能够用软件和硬件两种方法实现，并且有利于有效的固件实现；
  • 算法设计相对简单。

分组密码的填充与模式

（1）什么是填充，为什么需要填充

padding

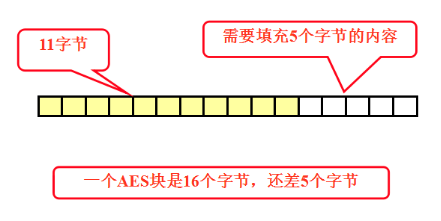
no padding

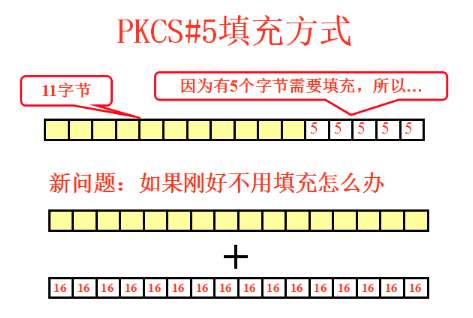
PKCS#5 padding

（2）什么是模式，为什么需要模式

mode

分组密码工作模式的应用背景：多次使用相同的密钥对多个分组加密，会引发许多安全问题。为了应对不同场合，因而需要开发出不同的工作模式来增强密码算法的安全性。

group work mode

  • ECB模式

    特别适合数据较少的情况，对于很长的信息或者具有特定结构的信息（对ECB模式分组重放攻击），其大量重复的信息或固定的字符开头将给密码分析者提供大量的已知明密文对。若明文不是完整的分组，ECB需要进行填充。

    ECB

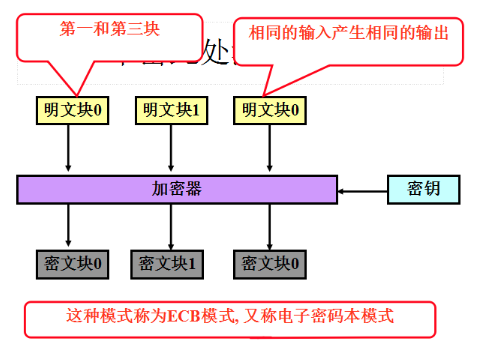
    ECB模式的特点

    • 简单
    • 有利于并行
    • 计算误差不会被传递
    • 不能隐藏明文的模式
    • 可能对明文进行主动攻击

  • CBC模式

    由于加密算法的每次输入和本明文组没有固定的关系，因此就算有重复的明文组，加密后也看不出来了。为了配合算法的需要，有一个初始向量（IV）。与ECB一样有填充机制以保证完整的分组。

    CBC

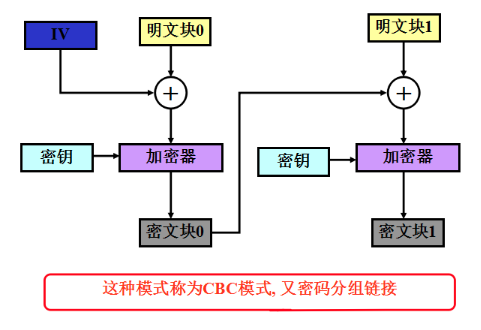
    CBC的特点

    • 不容易主动攻击
    • 不利于并行
    • 计算误差传递
    • 需要初始向量IV

    安全性好于ECB, 适合传输长度长的报文,是SSL, IPSec的标准

  • CFB模式

    和OFB，CTR模式一样，均可将分组密码当做流密码（实际是将分组大小任意缩减）使用。

    CFB

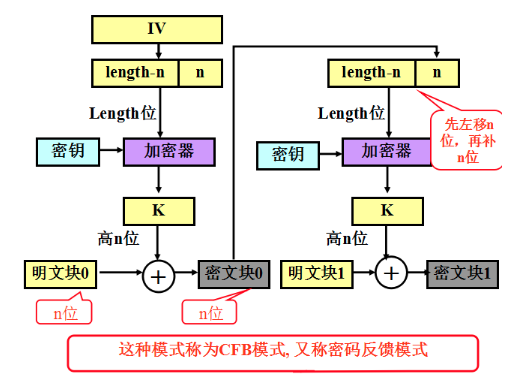
    CFB模式的特点

    • 隐藏了明文模式
    • 分组密码转化为流模式
    • 可以及时加密传输小于分组的数据
    • 不利于并行计算
    • 误差传递：一个明文单元损坏影响多个单元唯一的ＩＶ

  • OFB模式

    OFB的结构与CFB很相似，它用加密函数的输出填充移位寄存器，而CFB是用密文单元来填充移位寄存器。其他的不同是，OFB模式是对整个明文和密文分组进行运算，而不是仅对s位的子集运算，因而不至于浪费运算能力。

    OFB

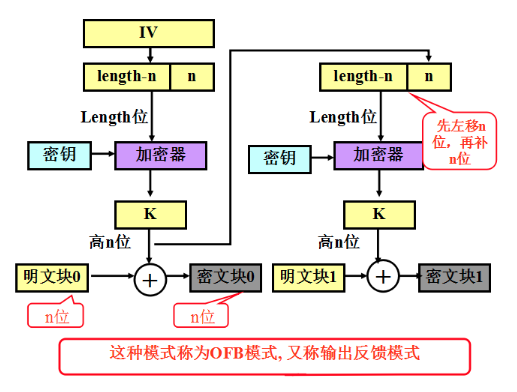
    OFB模式的特点

    • 隐藏了明文模式
    • 分组密码转化为流模式
    • 可以及时加密传输小于分组的数据
    • 不利于并行计算
    • 对明文的主动攻击是可能的
    • 误差传递：一个单元损坏只损坏对应单元
    • 唯一的ＩＶ

    安全性于不如CFB

流密码

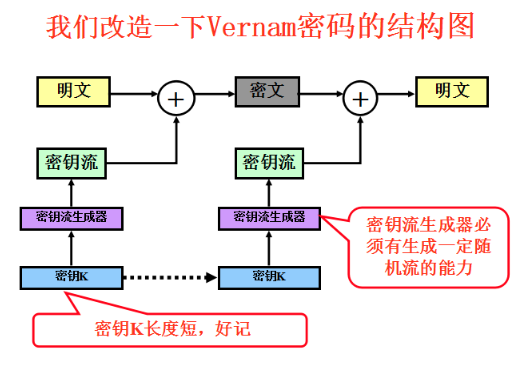
vernam

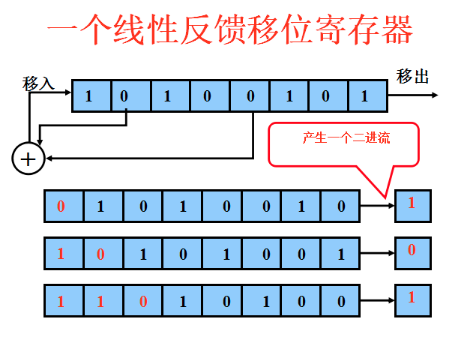
linear feedback shift register

随机位的测试

  • 单个位测试(monobit test) 目的：校验1和0的个数是否大致相等。
  • 扑克牌测试(poker test) 目的： 测试0至15的分布的随机随机性
  • 连续串测试 目的：测试连续串长度分布的随机性

单向散列函数

性质

  • h(x)的输入x为任意长度
  • h(x)的输出长度固定
  • h(x)的计算方便快捷
  • h(x)的计算具有单向性
  • 对于给定 x, 找到 y != x, 且 h(y) = h(x) 在计算不可行

应用

（1）使用Hash函数进行完整性验证的模型

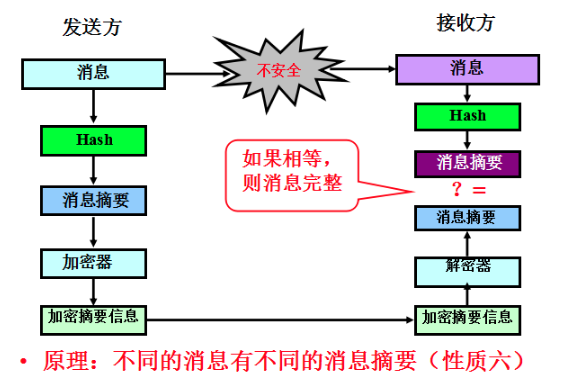
check integrity by hash

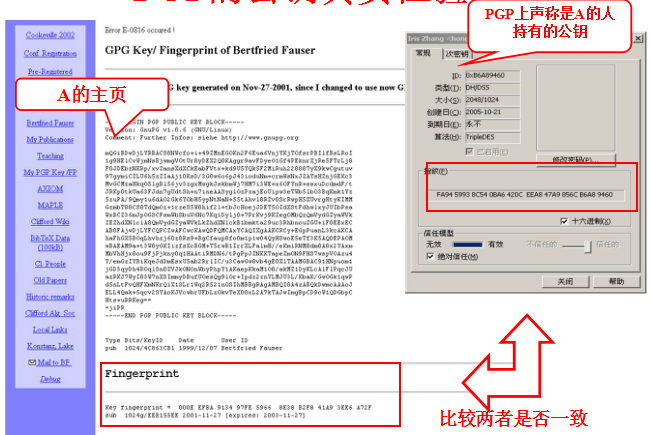
（2）PGP的公钥真实性验证

PGP public key verify

碰撞

如果 y != x, 且 h(x) = h(y), 则称为碰撞 对给定的 x, 要找到一个 y 满足 y != x, h(x) = h(y) 在计算上不可行, 则称为弱无碰撞 要找到任意一对数 x,y, y != x, 满足 h(x) = h(y), 在计算上不可行, 则称为强无碰撞(包含弱无撞)

hash collision

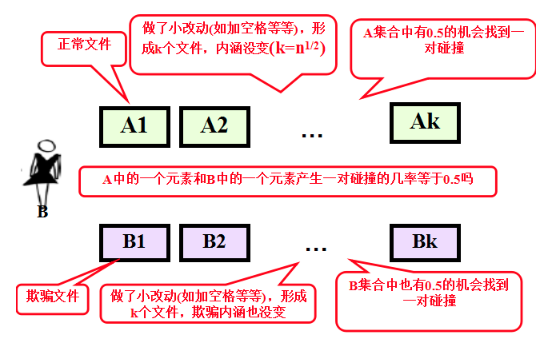
对数字签名的生日攻击

birthday attack

不对称密码

公钥密码的特性

  • 特性一：加密和解密使用不同的钥匙
  • 特性二：从一个钥匙推出另一个钥匙在计算上不可行
  • 特性三：每个钥匙都可以做加密和解密

RSA算法

RSA算法可用于加密、又可用于数字签字，易懂且易于实现，是目前仍然安全并且逐步被广泛应用的一种体制。

Euler函数

Euler function

Euler定理

Euler theorem

RSA密钥对生成步骤

RSA key pair generation

RSA加密和解密步骤

加密消息前，首先将它分成比n小的数据分组，再对每个分组加密

  • 加密： \(C=M^e(mod\ n)\)
  • 解密： \(M=C^d(mod\ n)\)

RSA密钥对生成实例

RSA key pair generation example

RSA encrypt and decrypt example

RSA的缺点

受到素数产生技术的限制，产生密钥很麻烦。 分组长度太大，为保证安全性，n 至少也要 600比特以上，使运算代价很高，尤其是速度较慢；且随着大数分解技术的发展，这个长度还在增加，不利于数据格式的标准化

当p,q比较接近的数分解攻击

decomposition attack 1

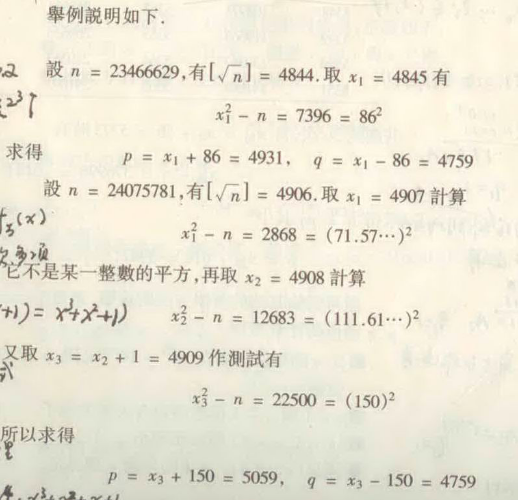
decomposition attack 2

选择明文攻击

select plaintext attack

从算法上无法解决这一问题，主要措施是采用好的公钥协议：

  • 工作过程中实体不轻易对其他实体任意产生的信息加解密，不对自己一无所知的信息签名
  • 对其他实体送来的随机文档签名时首先对文档作HASH处理

ElGamal密码体制

由ElGamal[1984,1985]提出，是一种基于离散对数问题的双钥密码体制，既可用于加密，又可用于签字。

ElGamal密钥对生成步骤

ElGamal key pair gen

ElGamal加密和解密步骤

ElGamal encrypt and decrypt

ElGamal密钥对生成例子

ElGamal key pair gen example

ElGamal加密和解密例子

ElGamal encrypt and decrypt example

Diffie-Hellman密钥交换

密钥交换方案:允许两个用户可以安全地建立一个秘密信息，用于后续的通讯过程 算法的安全性依赖于:有限域上计算离散对数的难度

DH密钥匙方案实现步骤

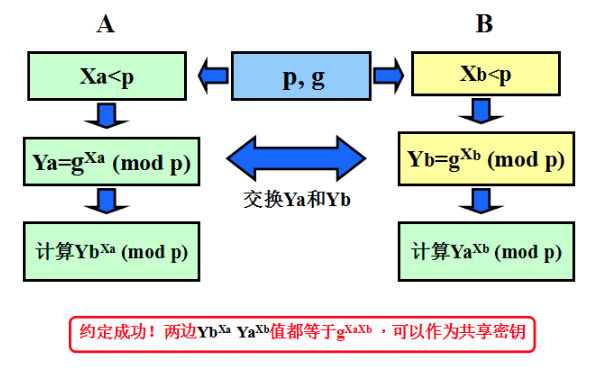
DH key exchange

DH密钥匙交换方案实现例子

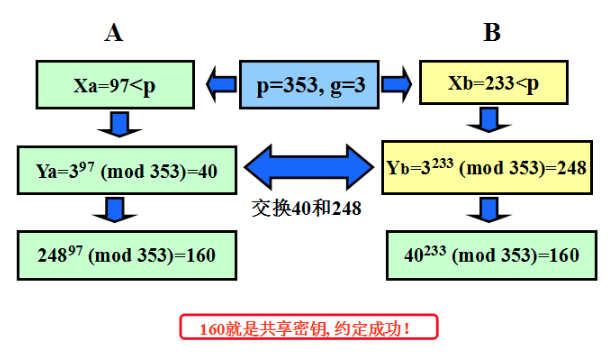
DH key exchange example

DH密钥匙方案的第三者攻击方法

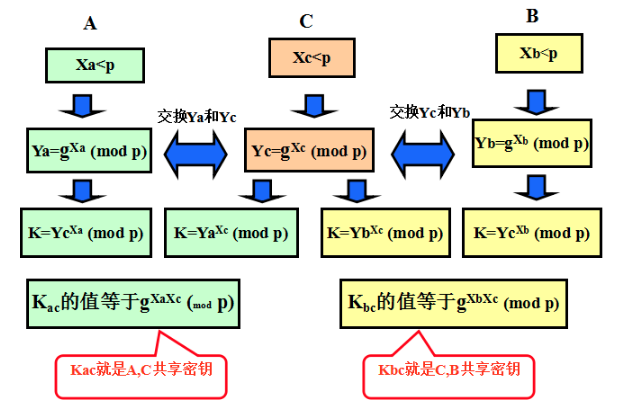
DH third party attack

第三者攻击的方法的为什么可以成功呢? 问题在于：A和B在不安全的信道上通信, 那么双方如何能够知道通信的另一方的到底是谁呢? 是否能设计一种可以确认通信双方身份的DH密钥交换方案呢?

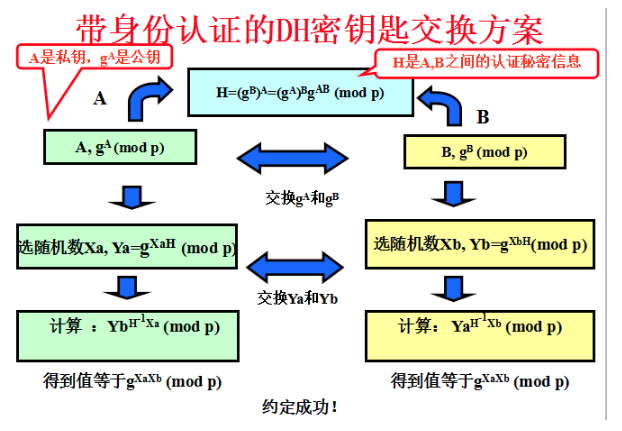
DH key exchange with identity auth

数字签名

RSA签名方案

RSA signature

RSA signature example

ELG签名方案

ELG signature

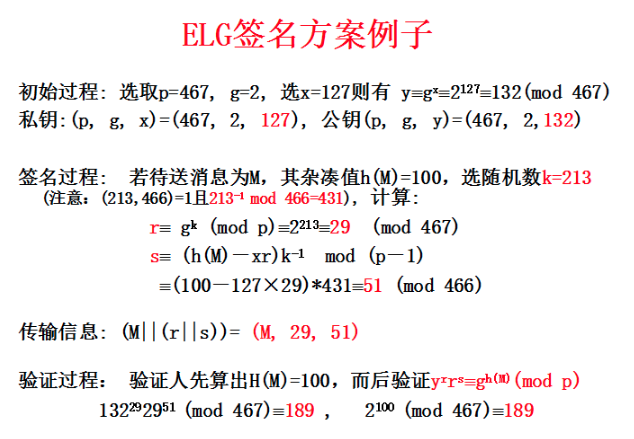
ELG signature example

实验02

（1）使用PGP软件，产生一对新的公钥/私钥，并在PGP服务器上注册

思考：为什么不是由服务器统一产生公钥/私钥对呢，而是由客户端产生钥匙对呢？注册完成后，公钥/私钥存放在什么地方呢？私钥需要什么样的保护措施吗？

  • 公钥/私钥对不由任一政府或标准化组织所控制，使得PGP得到广泛信任，能够满足商业化的需求。
  • 在服务器上注册后，公钥存放在服务器上，私钥则由使用者自己保存。
  • 使用口令密码对私钥加密存储，口令密码方便记忆，也可以保护私钥。

（2）邀请其他使用者互相签署对方的公钥

思考：此步骤的意义是什么？在签署他人的公钥前，应该注意什么？

  • 相互签署公钥用于建立信任体系，信任对方公钥是指定实体的合法公钥。
  • 需要确认所签署公钥是指定实体的合法公钥，可行的方法有：物理上得到对方的公钥，这种方式最可靠，但有一定局限性；通过电话验证公钥；从双方都信任的第三方处获得对方公钥。

（3）使用ASCII编码格式将自己的公钥发给其他使用者

思考：这样在整个PGP信任体系中的意义是什么？

  • 向信任的朋友发送公钥和接收信任朋友传送来的公钥，一般这些公钥都带有签名，在这种方式下，用户可以自行决定对周围的联系人是否信任，建立以个人为中心的信任模型。

（4）发送加密及签名的电子邮件

思考: 加密时使用了谁的、哪一把钥匙；签名时又使用了谁的、哪一把钥匙？邮件是否一定要同时加密和签名呢？邮件的长度是可变的，但数字签名的数据长度似乎是定长，这是为什么？

  • 加密时使用了接收者的公钥
  • 签名时使用了发送者的私钥
  • 邮件不一定要同时加密和签名
  • 实际上，sign & verify 是利用 hash function 及非对称加密的技术来达到确认文件来源及文件内容是没被更改过的，而hash value的长度是由不同的hash function决定的，常见的hash function有MD2, MD5, SHA-1, SHA-128, SHA-256, SHA-512

（5）收到他人的加密及签名的电子邮件后，解密并验证其签名的正确性

思考：解密时使用了谁的、哪一把钥匙；验证签名时又使用了谁的、哪一把钥匙？

  • 解密时使用了接收者的私钥
  • 验证签名时使用了发送者的公钥