MergeSort

归并排序（Merge sort），是创建在归并操作上的一种基于比较的排序算法。1945 年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

归并排序（Merge sort）

基本原理

归并排序算法是分治策略实现对 n 个元素进行排序的算法。

其基本思想是：将待排序元素分成大小大致相同的 2 个子集合，分别对 2 个子集合进行排序，最终将排好序的子集合合并成为所要求的排好序的集合。

算法步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤 3 直到某一指针到达序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

算法图解

参考 dreamcatcher-cx 博客 图解排序算法(四)之归并排序

采用经典的分治（divide-and-conquer）策略（分治法将问题分解成规模更小、解法相同的子问题，然后通过子问题的解构造出原问题的解)。

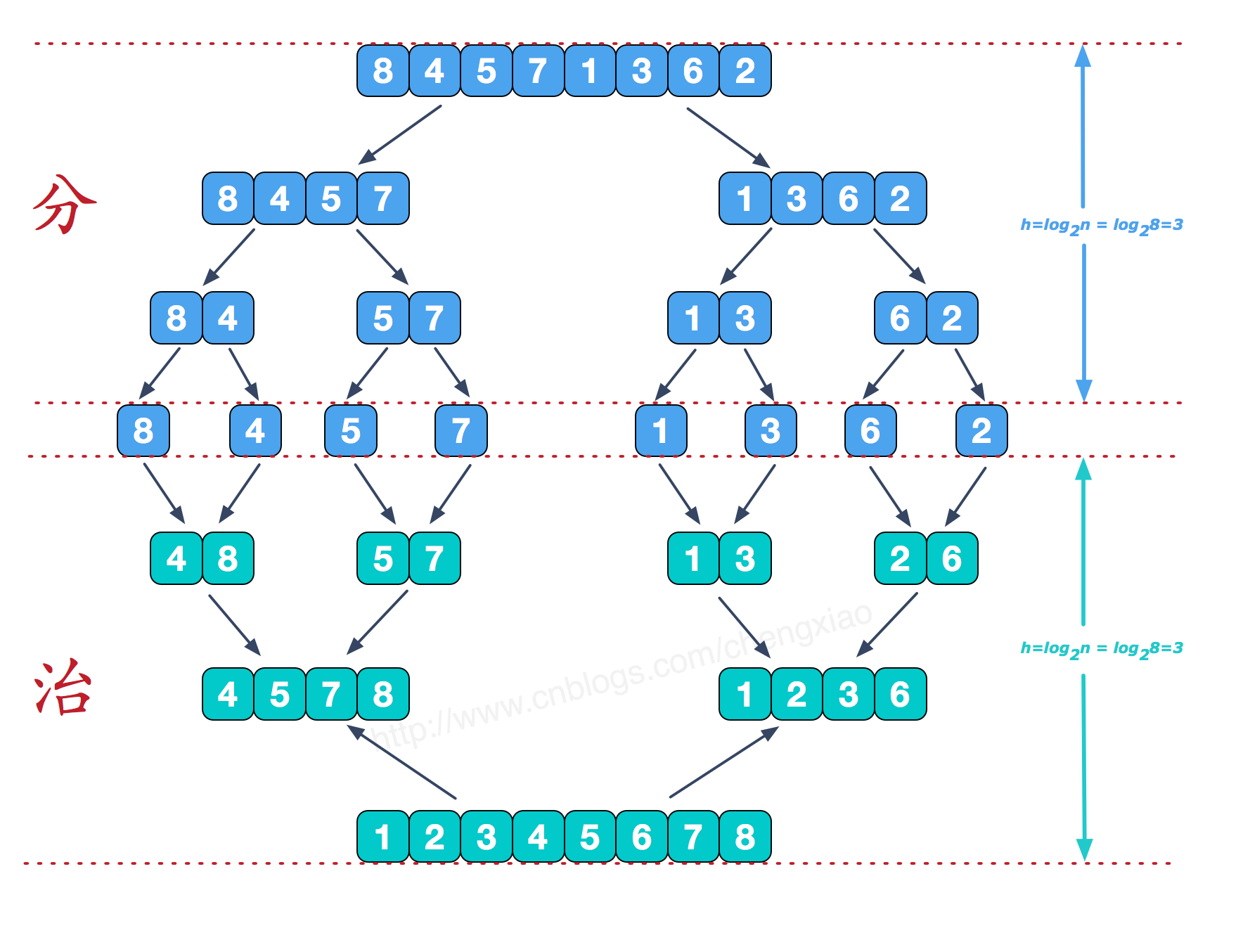
分阶段是递归拆分子序列的过程，递归深度为 \(log_2 n\).

对于治阶段，需要将两个已经有序的子序列合并成一个有序序列，例如上图中的最后一次合并，要将 [4,5,7,8] 和 [1,2,3,6] 两个已经有序的子序列，合并为最终序列 [1,2,3,4,5,6,7,8] ，具体实现步骤如下:

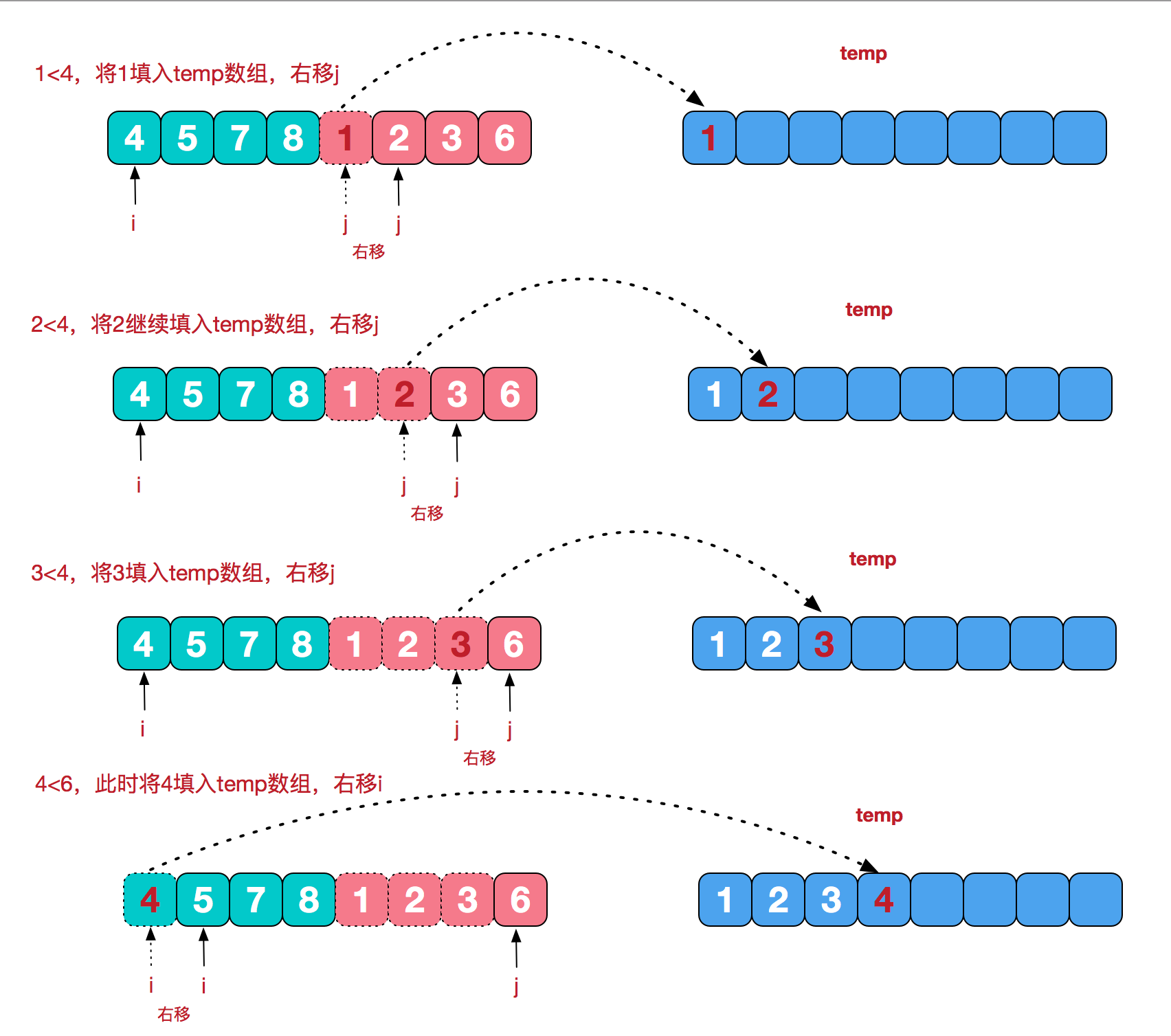
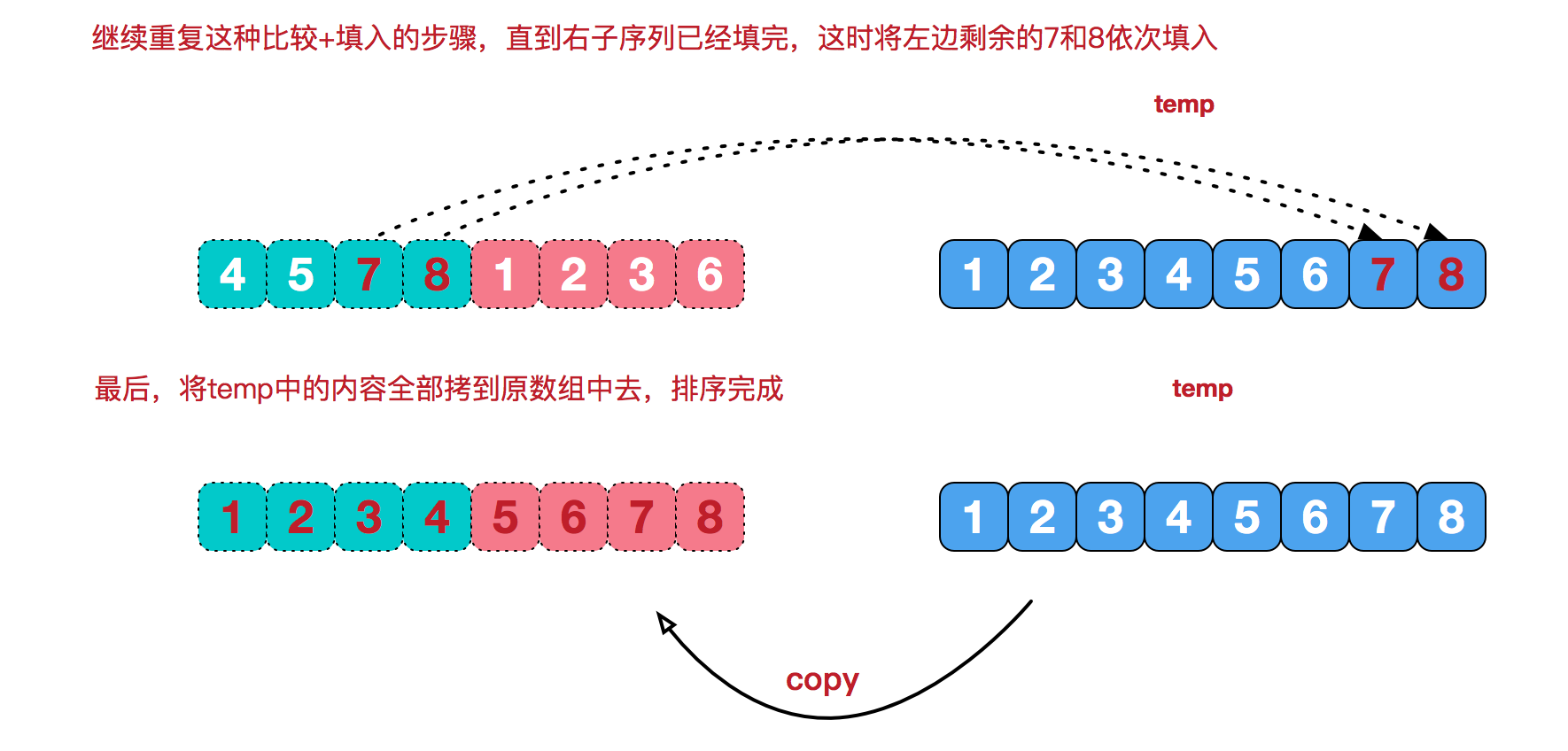
动画演示

参考实现

import java.util.Arrays;

/**
 * @author wylu
 */
public class MergeSort {

    public static void merge(int[] arr, int left, int mid, int right, int[] tmp) {
        int i = left, j = mid + 1, t = 0;
        while (i <= mid && j <= right) tmp[t++] = (arr[i] <= arr[j]) ? arr[i++] : arr[j++];
        while (i <= mid) tmp[t++] = arr[i++];
        while (j <= right) tmp[t++] = arr[j++];
        t = 0;
        while (left <= right) arr[left++] = tmp[t++];
    }

    //递归
    public static void recursiveSort(int[] arr, int left, int right, int[] tmp) {
        if (left < right) {
            int mid = (left + right) / 2;
            recursiveSort(arr, left, mid, tmp);
            recursiveSort(arr, mid + 1, right, tmp);
            merge(arr, left, mid, right, tmp);
        }
    }

    //非递归
    public static void nonRecursiveSort(int[] arr) {
        int[] tmp = new int[arr.length];
        for (int size = 1; size < arr.length; size *= 2) {
            int left, mid, right;
            for (left = 0; left + size < arr.length; left = right + 1) {
                mid = left + size - 1;
                right = Math.min(mid + size, arr.length - 1);
                merge(arr, left, mid, right, tmp);
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 4, 9, 6, 0, 7, 2, 5, 8};
//        MergeSort.recursiveSort(arr, 0, arr.length - 1, new int[arr.length]);
        MergeSort.nonRecursiveSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

复杂度分析

排序算法	平均时间复杂度	最好情况	最坏情况	空间复杂度	排序方式	稳定性
归并排序	\(O(nlogn)\)	\(O(nlogn)\)	\(O(nlogn)\)	\(O(n)\)	Out-place	稳定

References

https://en.wikipedia.org/wiki/Merge_sort

https://www.cnblogs.com/chengxiao/p/6194356.html

https://youliao.163yun.com/api-server/rss/xiaomi/item/IN2WDOMKAWVNTZV.html?ref=browser_news&s=mb&cp=cn-netease-youliao-browser&docid=44797c69e120935b2c4790d933d02a9b&itemtype=news&cateCode=rec&category=%E7%A7%91%E6%8A%80