在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

• Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
• Union：将两个子集合并成同一个集合。

由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（union-find data structure）或合并-查找集合（merge-find set）。其他的重要方法，MakeSet，用于建立单元素集合。有了这些方法，许多经典的划分问题可以被解决。

并查集

并查集是什么

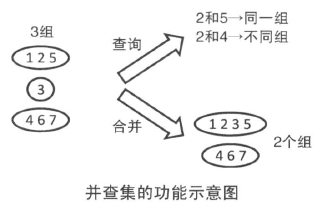
并查集是一种用来管理元素分组情况的数据结构。并查集可以高效地进行如下操作。不过需要注意并查集虽然可以进行合并操作，但是却无法进行分割操作。

• 查询元素 a 和元素 b 是否属于同一组。
• 合并元素 a 和元素 b 所在的组。

并查集的结构

并查集也是树形结构实现的。不过，不是二叉树。

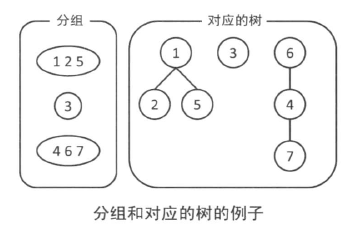
每个元素对应一个节点，每个组对应一棵树。在并查集中，哪个节点是哪个节点的父亲以及树的形状等信息无需多加关注，整体组成一个树形结构才是重要的。

（1）初始化

我们准备 n 个节点来表示 n 个元素。最开始时没有边。

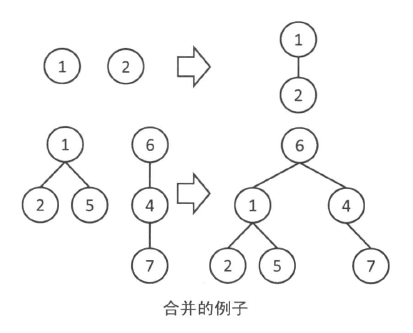
（2）合并

像下图一样，从一个组的根向另一个组的根连边，这样两棵树就变成了一棵树，也就把两个组合并为一个组了。

（3）查询

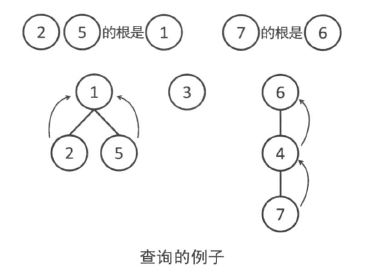
为了查询两个节点是否属于同一组，我们需要沿着树向上走，来查询包含这个元素的树的根是谁。如果两个节点走到了同一个根，那么就可以知道它们属于同一组。

在下图中，元素 2 和元素 5 都走到了元素 1，因此它们属于同一组。另一方面，由于元素 7 走到的是元素 6，因此同元素 2 或元素 5 属于不同组。

并查集实现中的注意点

在树形数据结构里，如果发生了退化的情况，那么复杂度就会变得很高。因此，有必要想办法避免退化的发生。在并查集中，只需按照如下方法就可以避免退化。

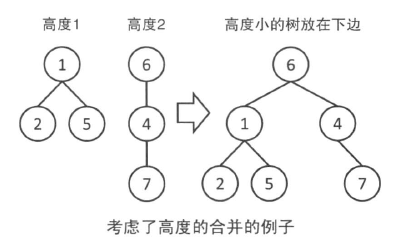
• 对于每棵树，记录这棵树的高度(rank)。
• 合并时如果两棵树的 rank 不同，那么从 rank 小的向 rank 大的连边。

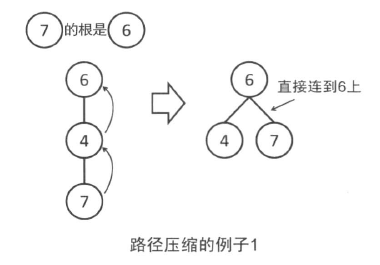
此外，通过路径压缩，可以使得并查集更加高效。对于每个节点，一旦向上走到了一次根节点，就把这个点到父亲的边改为直接连向根。

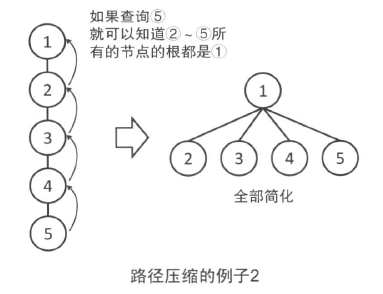
在此之上，不仅仅是所查询的节点，在查询过程中向上经过的所有的节点，都改为直接连到根上。这样再次查询这些节点时，就可以很快知道根是谁了。

在使用这种简化的方法时，为了简单起见，即使树的高度发生了变化，我们也不修改 rank 的值。

并查集的复杂度

加入了这两个优化之后的并查集效率非常高。对 n 个元素的并查集进行一次操作的复杂度是 \(O(\alpha(n))\)。在这里，\(\alpha(n)\) 是阿克曼( Ackermann )函数的反函数。这比 \(O(log(n))\) 还要快。

不过，这是“均摊复杂度”。也就是说，并不是每一次操作都满足这个复杂度，而是多次操作之后平均每一次操作的复杂度是 \(O(\alpha(n))\) 的意思。

并查集的实现

下面是并查集的实现的例子。在例子中，我们用编号代表每个元素。数组 par 表示的是父亲的编号，par[x] = x 时, x 是所在的树的根。

路径压缩

class UnionFind:
    def __init__(self, n: int):
        self.par = list(range(n))

    def find(self, x: int) -> int:
        if self.par[x] != x:
            self.par[x] = self.find(self.par[x])
        return self.par[x]

    def union(self, x: int, y: int) -> None:
        self.par[self.find(x)] = self.find(y)

路径压缩 + 按秩（rank）合并

class UnionFind:
    # 初始化 n 个元素
    def __init__(self, n: int):
        self.par = list(range(n))  # 祖先结点
        self.rank = [0] * n  # 树的高度

    # 查询树的根
    def find(self, x: int) -> int:
        if self.par[x] != x:
            self.par[x] = self.find(self.par[x])
        return self.par[x]

    # 合并 x 和 y 所属的集合
    def union(self, x: int, y: int) -> None:
        x = self.find(x)
        y = self.find(y)
        if x == y:
            return

        if self.rank[x] < self.rank[y]:
            self.par[x] = y
        else:
            self.par[y] = x
            if self.rank[x] == self.rank[y]:
                self.rank[x] += 1

References

https://en.wikipedia.org/wiki/Disjoint-set_data_structure

<<挑战程序设计竞赛(第2版)>> 巫泽俊 2.4 并查集 p84-88