递归地解决树问题

发表于 更新于 分类于 ， 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

在前面的部分中，我们介绍了如何递归解决树遍历问题。递归是解决树问题的最强大，最常用的技术之一。

众所周知，树可以递归定义为一个节点（根节点），该节点包含一个值和对子节点的引用列表。递归是树的自然特征之一。因此，许多树问题可以递归解决。对于每个递归函数调用，我们仅关注当前节点的问题，然后递归调用函数以解决其子级。

通常，我们可以使用 自上而下 的方法或 自下而上 的方法递归地解决树问题。

递归地解决树问题

自上而下的解决方案

“自顶向下”表示在每个递归调用中，我们将首先访问该节点以提供一些值，并在递归调用该函数时将这些值传递给其子级。因此，“自上而下”的解决方案可以看作是一种前序遍历（preorder traversal）。具体来说，递归函数 top_down(root, params) 的工作方式如下：

1
2
3
4
5
1. return specific value for null node
2. update the answer if needed                      // answer <-- params
3. left_ans = top_down(root.left, left_params)      // left_params <-- root.val, params
4. right_ans = top_down(root.right, right_params)   // right_params <-- root.val, params
5. return the answer if needed                      // answer <-- left_ans, right_ans

例如，考虑以下问题：给定一棵二叉树，找到其最大深度。

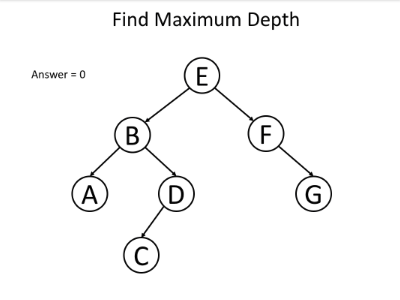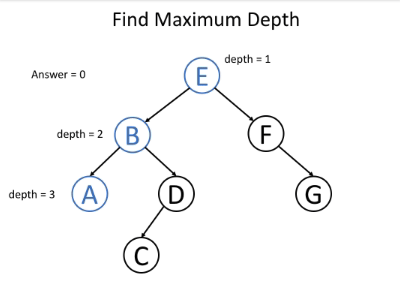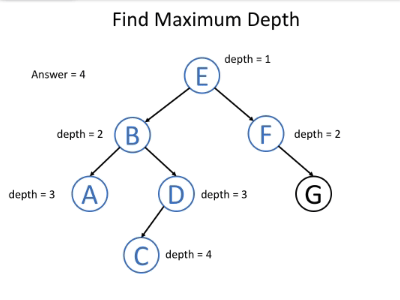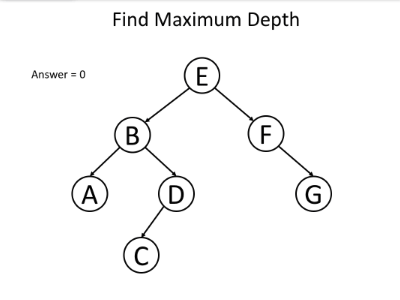
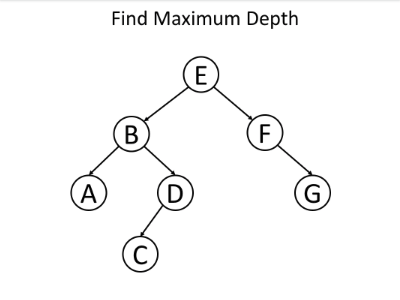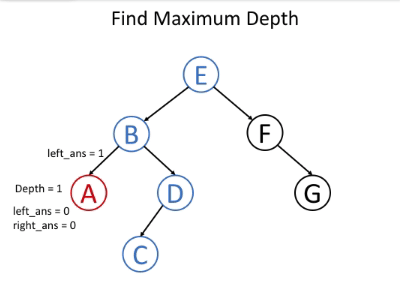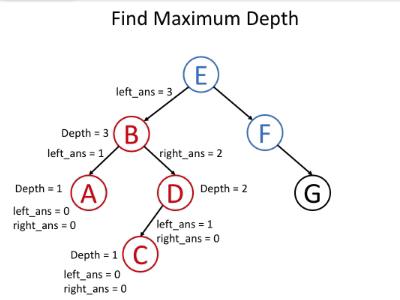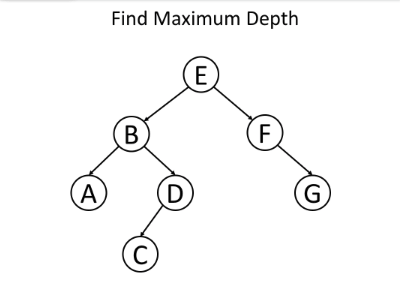
我们知道根节点的深度为1。对于每个节点，如果我们知道其深度，我们将知道其子节点的深度。因此，如果在递归调用函数时将节点的深度作为参数传递，则所有节点都将知道其深度。对于叶节点，我们可以使用深度来更新最终答案。这是递归函数 maximum_depth(root, depth) 的伪代码：

1
2
3
4
5
1. return if root is null
2. if root is a leaf node:
3.      answer = max(answer, depth)         // update the answer if needed
4. maximum_depth(root.left, depth + 1)      // call the function recursively for left child
5. maximum_depth(root.right, depth + 1)     // call the function recursively for right child

以下示例可帮助您了解其工作原理：

top-down-solution

Java 参考代码：

1
2
3
4
5
6
7
8
9
10
11
private int answer;  // don't forget to initialize answer before call maximum_depth
private void maximum_depth(TreeNode root, int depth) {
    if (root == null) {
        return;
    }
    if (root.left == null && root.right == null) {
        answer = Math.max(answer, depth);
    }
    maximum_depth(root.left, depth + 1);
    maximum_depth(root.right, depth + 1);
}

自下而上的解决方案

“自底而上”是另一种递归解决方案。在每个递归调用中，我们将首先对所有子节点递归调用该函数，然后根据返回的值和当前节点本身的值得出答案。此过程可以视为一种后序遍历（postorder traversal）。通常，“自下而上”的递归函数 bottom_up(root) 将是这样的：

1
2
3
4
1. return specific value for null node
2. left_ans = bottom_up(root.left)          // call function recursively for left child
3. right_ans = bottom_up(root.right)        // call function recursively for right child
4. return answers                           // answer <-- left_ans, right_ans, root.val

让我们继续讨论有关最大深度的问题，但使用另一种思考方式：对于树的单个节点，以自身为根的子树的最大深度 x 将是多少？

如果我们知道以其左孩子为根的子树的最大深度 l 和以其右孩子为根的子树的最大深度 r，我们可以回答前面的问题吗？当然可以，我们可以选择它们之间的最大值，然后加1以获取根于当前节点的子树的最大深度。即 x = max(l, r) + 1。

这意味着对于每个节点，我们都可以在为其子节点解决问题后得到答案。因此，我们可以使用“自下而上”的解决方案来解决此问题。这是递归函数 maximum_depth(root) 的伪代码：

1
2
3
4
1. return 0 if root is null                 // return 0 for null node
2. left_depth = maximum_depth(root.left)
3. right_depth = maximum_depth(root.right)
4. return max(left_depth, right_depth) + 1  // return depth of the subtree rooted at root

以下示例可帮助您了解其工作原理：

bottom-up-solution

Java 参考代码：

1
2
3
4
5
6
7
8
public int maximum_depth(TreeNode root) {
    if (root == null) {
        return 0;  // return 0 for null node
    }
    int left_depth = maximum_depth(root.left);
    int right_depth = maximum_depth(root.right);
    return Math.max(left_depth, right_depth) + 1;  // return depth of the subtree rooted at root
}

总结

理解递归并找到该问题的递归解决方案并不容易。它需要练习。

遇到树型问题时，请问自己两个问题：是否可以确定一些参数来帮助节点知道其答案？您可以使用这些参数和节点本身的值来确定将什么参数传递给它的子节点吗？如果答案都是肯定的，请尝试使用“自顶向下”递归解决方案来解决此问题。

或者，您可以通过这种方式思考问题：对于树中的某个节点，如果您知道其子节点的答案，可以计算该节点的答案吗？如果答案是肯定的，那么使用自下而上的方法递归解决问题可能是一个好主意。

在下面，我们为您提供了几个经典问题，以帮助您更好地理解树的结构和递归。

二叉树节点定义

  • java
1
2
3
4
5
6
7
// Definition for a binary tree node.
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}
  • python
1
2
3
4
5
6
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

二叉树递归练习

二叉树的最大深度

给定二叉树，找到其最大深度。

最大深度是沿着从根节点到最远叶节点的最长路径的节点数。

注意：叶是没有子节点的节点。

例：给定二叉树[3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其深度 = 3

java 参考代码：

1
2
3
4
5
6
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

python 参考代码：

1
2
3
4
5
6
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

对称二叉树

给定一棵二叉树，检查它是否是其自身的镜像（即，围绕其中心对称）。

例如，此二叉树[1,2,2,3,4,4,3]是对称的：

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

但[1,2,2,null,3,null,3]不是：

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

递归和迭代地解决它。

java 参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    /**
     * 递归地判断左右子树是否对称
     * @param r1 左子树根结点
     * @param r2 右子树根结点
     * @return bool
     */
    private boolean recursive(TreeNode r1, TreeNode r2) {
        if (r1 == null && r2 == null) return true;
        if (r1 == null || r2 == null) return false;
        return (r1.val == r2.val) && recursive(r1.left, r2.right) && recursive(r1.right, r2.left);
    }

    /**
     * 迭代地判断树是否对称
     * @param root 树的根结点
     * @return bool
     */
    private boolean iterate(TreeNode root) {
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode r1 = queue.poll();
            TreeNode r2 = queue.poll();
            if (r1 == null && r2 == null) continue;
            if (r1 == null || r2 == null || r1.val != r2.val) return false;
            queue.offer(r1.left);
            queue.offer(r2.right);
            queue.offer(r1.right);
            queue.offer(r2.left);
        }
        return true;
    }

    public boolean isSymmetric(TreeNode root) {
//        if (root == null) return true;
//        return recursive(root.left, root.right);
        return iterate(root);
    }
}

python 参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        return self.isSym(root, root)

    def isSym(self, r1: TreeNode, r2: TreeNode) -> bool:
        if not r1 and not r2:
            return True

        if not r1 or not r2:
            return False

        return (r1.val == r2.val and self.isSym(r1.left, r2.right)
                and self.isSym(r1.right, r2.left))

路径总和

给定一个二叉树和一个和，确定该树是否具有从根到叶的路径，以使该路径上的所有值加起来等于给定的和。

注意：叶是没有子节点的节点。

例：给定下面的二叉树，并且 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

返回true，因为存在从根到叶的路径 5->4->11->2，其总和为22。

java 参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) return false;
        return hasPathSum(root, sum, 0);
    }

    private boolean hasPathSum(TreeNode root, int sum, int cur) {
        cur += root.val;
        if (root.left == null && root.right == null) return sum == cur;
        boolean flag = false;
        if (root.left != null) flag = hasPathSum(root.left, sum, cur);
        if (!flag && root.right != null) flag = hasPathSum(root.right, sum, cur);
        return flag;
    }
}

python 参考代码：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
        if not root:
            return False

        if not root.left and not root.right:
            return root.val == sum

        return (self.hasPathSum(root.left, sum - root.val)
                or self.hasPathSum(root.right, sum - root.val))

References

https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/534/

https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/535/

https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/536/

https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/537/