了解树和二叉树的相关概念;
理解不同遍历方法的工作原理,掌握相应遍历方法的递归和迭代实现;
二叉树
树和二叉树的概念
树是模拟分层树结构的常用数据结构。
树的每个节点将具有一个根值和包含其它被称为子节点的引用列表。从图的角度来看,树也可以定义为具有 N 个节点和 N-1 个边的有向无环图。
二叉树是最典型的树结构之一。顾名思义,二叉树是一种树数据结构,其中每个节点最多具有两个孩子节点,分别称为左孩子和右孩子。
二叉树节点定义
1
2
3
4
5
6
7
|
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
|
1
2
3
4
5
6
|
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
|
树的遍历
本文的目的:
了解不同的树遍历方法之间的区别;
能够递归地解决前序,中序和后序遍历;
能够迭代解决前序,中序和后序遍历;
能够使用 BFS 进行分层遍历。
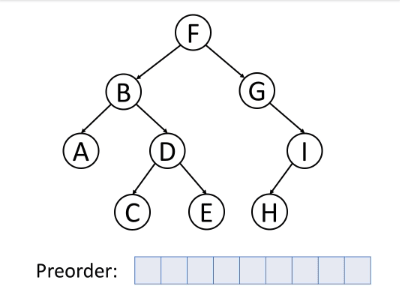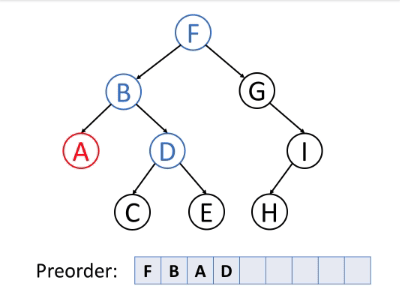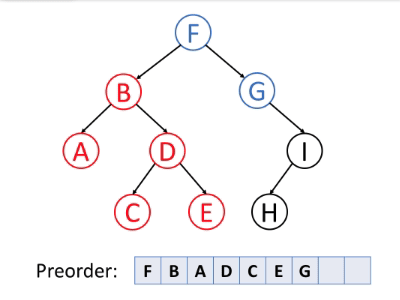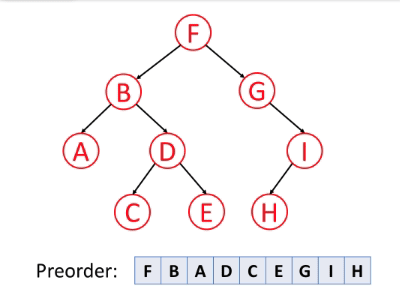
前序遍历(Preorder Traversal)
前序遍历是首先访问根,然后遍历左子树,最后遍历右子树。
例题
给定一个二叉树,返回其节点值的前序遍历序列。
Example:
1
2
3
4
5
6
7
8
| Input: [1,null,2,3]
1
\
2
/
3
Output: [1,2,3]
|
递归
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
private void recursive(TreeNode root, List<Integer> res) {
if (root == null) return;
res.add(root.val);
recursive(root.left, res);
recursive(root.right, res);
}
public List<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
recursive(root, res);
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| from typing import List
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
return self.recursiveTraversal(root)
def recursiveTraversal(self, root: TreeNode) -> List[int]:
res = []
self.recursive(root, res)
return res
@classmethod
def recursive(cls, root: TreeNode, res: List[int]) -> None:
if not root:
return
res.append(root.val)
cls.recursive(root.left, res)
cls.recursive(root.right, res)
|
迭代
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
if (root == null) return res;
LinkedList<TreeNode> stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
root = stack.pop();
res.add(root.val);
if (root.right != null) stack.push(root.right);
if (root.left != null) stack.push(root.left);
}
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| from typing import List
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
return self.iterateTraversal(root)
def iterateTraversal(self, root: TreeNode) -> List[int]:
return self.iterate(root)
@classmethod
def iterate(cls, root: TreeNode) -> List[int]:
"""迭代地进行前序遍历
创建一个辅助栈:
1.将根结点压入栈
2.弹出栈顶结点,将结点值追加到结果序列的尾部
3.然后先将右子结点压入栈中(如果有)
4.再将左子结点压入栈中(如果有)
5.重复步骤2、3、4,直至栈空
Args:
root (TreeNode): 树的根结点
Returns:
List[int]: 前序遍历结果
"""
res = []
if not root:
return res
stack = [root]
while stack:
root = stack.pop()
res.append(root.val)
if root.right:
stack.append(root.right)
if root.left:
stack.append(root.left)
return res
|
中序遍历(Inorder Traversal)
中序遍历是首先遍历左子树,然后访问根,最后遍历右子树。
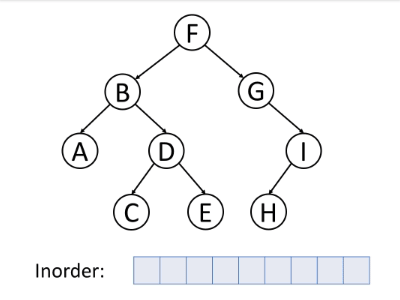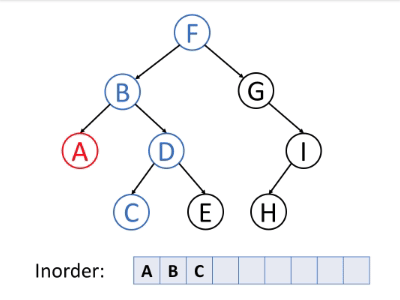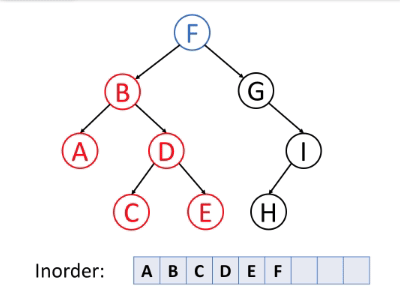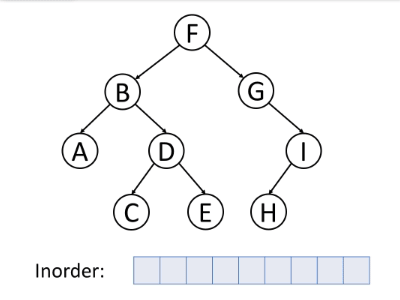
通常,对于二叉搜索树,我们可以使用中序遍历以排序的顺序检索所有数据。
例题
给定一个二叉树,返回其节点值的中序遍历序列。
Example:
1
2
3
4
5
6
7
8
| Input: [1,null,2,3]
1
\
2
/
3
Output: [1,3,2]
|
递归
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
private void recursive(TreeNode root, List<Integer> res) {
if (root == null) return;
recursive(root.left, res);
res.add(root.val);
recursive(root.right, res);
}
public List<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
recursive(root, res);
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| from typing import List
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
return self.recursiveTraversal(root)
def recursiveTraversal(self, root: TreeNode) -> List[int]:
res = []
self.recursive(root, res)
return res
@classmethod
def recursive(cls, root: TreeNode, res: List[int]) -> None:
if not root:
return
cls.recursive(root.left, res)
res.append(root.val)
cls.recursive(root.right, res)
|
迭代
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
if (root == null) return res;
LinkedList<TreeNode> stack = new LinkedList<>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
res.add(root.val);
root = root.right;
}
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| from typing import List
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
return self.iterateTraversal(root)
def iterateTraversal(self, root: TreeNode) -> List[int]:
return self.iterate(root)
@classmethod
def iterate(cls, root: TreeNode) -> List[int]:
"""迭代地进行中序遍历
创建一个辅助栈:
1.当前结点置为根结点
2.如果当前结点不为空,则将最左路径的所有结点压入栈中
3.弹出栈顶结点作为当前结点,将结点值追加到结果序列的尾部
4.然后将当前结点置为当前结点的右子结点
5.重复步骤2、3、4,直至当前结点为空且栈空
Args:
root (TreeNode): 树的根结点
Returns:
List[int]: 中序遍历结果
"""
res = []
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
res.append(root.val)
root = root.right
return res
|
后序遍历(Postorder Traversal)
后序遍历是首先遍历左子树,然后遍历右子树,最后访问根。
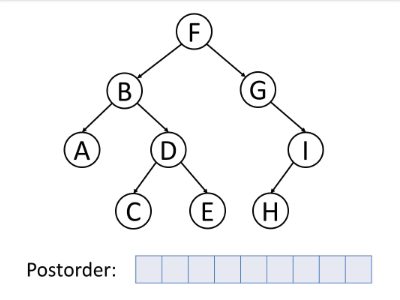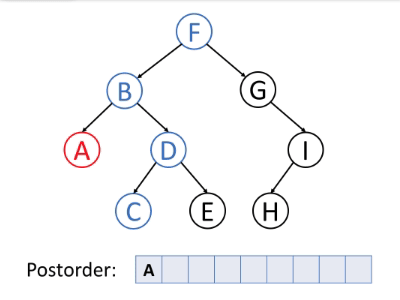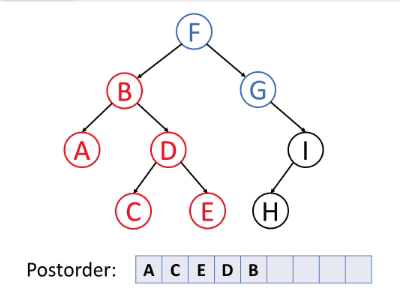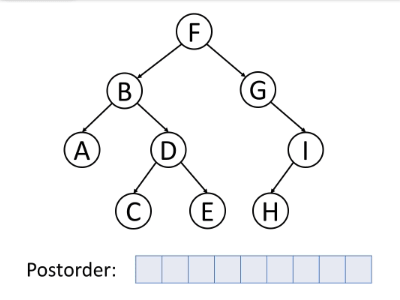
值得注意的是,当删除树中的节点时,删除过程应处于后序遍历状态。也就是说,删除节点时,先删除左节点,再删除右节点,然后再删除节点本身。
而且,后序在数学表达式中被广泛使用,编写程序来解析后序表达式会更容易。这是一个例子:
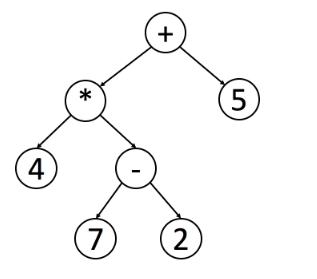
你可以使用中序遍历轻松找出原始表达式,但是,程序要处理该表达式(中序表达式)并不容易,因为你必须检查操作的优先级。
如果按后序处理此树,则可以使用栈轻松处理表达式,每次遇到操作符时,只需从栈中弹出 2 个元素,计算结果并将结果推回栈中即可。
例题
给定一个二叉树,返回其节点值的后序遍历序列。
Example:
1
2
3
4
5
6
7
8
| Input: [1,null,2,3]
1
\
2
/
3
Output: [3,2,1]
|
递归
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
private void recursive(TreeNode root, List<Integer> res) {
if (root == null) return;
recursive(root.left, res);
recursive(root.right, res);
res.add(root.val);
}
public List<Integer> postorderTraversal(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
recursive(root, res);
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| from typing import List
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
return self.recursiveTraversal(root)
def recursiveTraversal(self, root: TreeNode) -> List[int]:
res = []
self.recursive(root, res)
return res
@classmethod
def recursive(cls, root: TreeNode, res: List[int]) -> None:
if not root:
return
cls.recursive(root.left, res)
cls.recursive(root.right, res)
res.append(root.val)
|
迭代
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
LinkedList<TreeNode> stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
root = stack.pop();
res.addFirst(root.val);
if (root.left != null) stack.push(root.left);
if (root.right != null) stack.push(root.right);
}
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| from typing import List
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
return self.iterateTraversal(root)
def iterateTraversal(self, root: TreeNode) -> List[int]:
return self.iterate(root)
@classmethod
def iterate(cls, root: TreeNode) -> List[int]:
"""迭代地进行后序遍历
创建一个辅助栈:
1.将根结点压入栈
2.弹出栈顶结点,将结点值插入结果序列的头部
3.然后先将左子结点压入栈中(如果有)
4.再将右子结点压入栈中(如果有)
5.重复步骤2、3、4,直至栈空
Args:
root (TreeNode): 树的根结点
Returns:
List[int]: 后序遍历结果
"""
res = []
if not root:
return res
stack = [root]
while stack:
root = stack.pop()
res.append(root.val)
if root.left:
stack.append(root.left)
if root.right:
stack.append(root.right)
res.reverse()
return res
|
层次遍历(Level Order Traversal)
层次遍历是逐级遍历树,每一层从左往右依次遍历结点。
广度优先搜索(Breadth-First Search)是一种遍历或搜索数据结构(如树或图)的算法。该算法从根节点开始,并首先访问该节点本身。然后遍历其邻居,遍历其第二级邻居,遍历其第三级邻居,依此类推。
当我们在树中进行广度优先搜索(BFS)时,我们访问的节点的顺序是层次遍历的顺序。
这是一个层次遍历的示例:
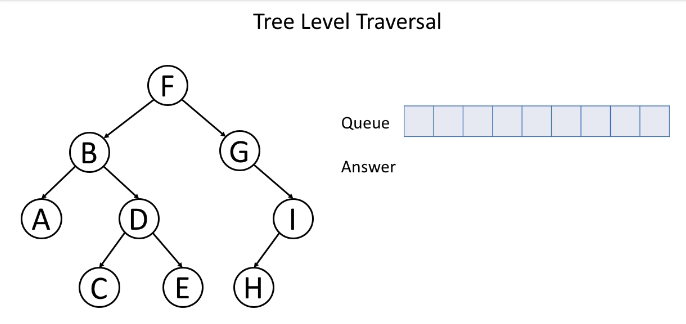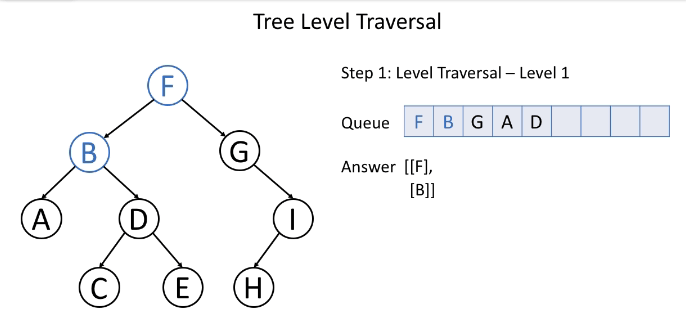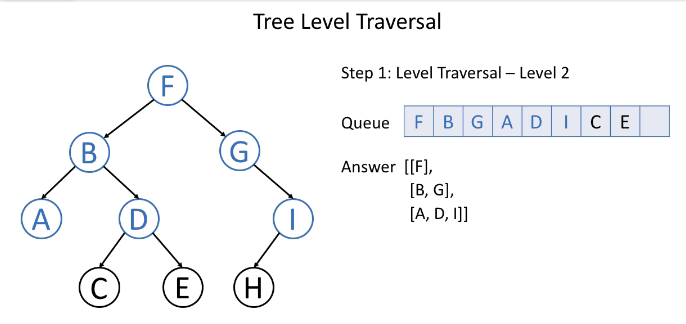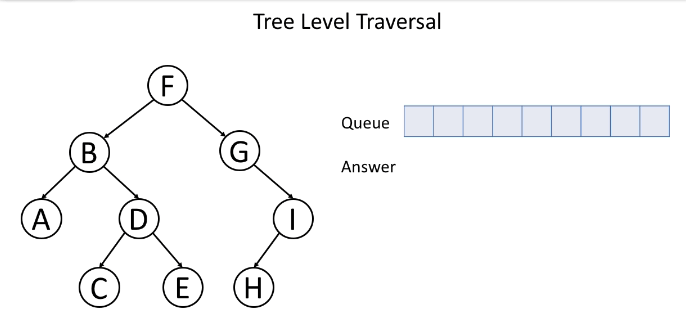
通常,我们使用队列来帮助我们进行BFS。
例题
给定一个二叉树,返回其节点值的层次遍历序列。(即,从左到右,逐级)。
Example:
给定一棵二叉树 [3,9,20,null,null,15,7]
返回其层次遍历结果为:
1
2
3
4
5
| [
[3],
[9,20],
[15,7]
]
|
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
List<Integer> level = new ArrayList<>();
TreeNode curTail = root, nextTail = null;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
level.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
nextTail = cur.left;
}
if (cur.right != null) {
queue.offer(cur.right);
nextTail = cur.right;
}
if (cur == curTail) {
res.add(level);
level = new ArrayList<>();
curTail = nextTail;
}
}
return res;
}
}
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| from collections import deque
from typing import List
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
ans = []
que = deque()
que.append(root)
while que:
level, size = [], len(que)
for _ in range(size):
root = que.popleft()
level.append(root.val)
if root.left:
que.append(root.left)
if root.right:
que.append(root.right)
ans.append(level)
return ans
|
References
https://leetcode.com/explore/learn/card/data-structure-tree/
https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/928/
https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/929/
https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/930/
https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/931/




