堆（Heap）是计算机科学中的一种特别的树状数据结构。若是满足以下特性，即可称为堆：“给定堆中任意节点 P 和 C，若 P 是 C 的母节点，那么 P 的值会小于等于（或大于等于） C 的值”。

堆始于 J._W._J._Williams 在 1964 年发表的堆排序（heap sort），当时他提出了二叉堆树作为此算法的数据结构。堆在 Dijkstra 等几种有效的图形算法中也非常重要。

堆是一种称为优先级队列的抽象数据类型的最有效实现，实际上优先级队列通常被称为“堆”，而不管它们如何实现。

堆 堆排序 优先队列

堆

严格来说，堆也有不同的种类。本文所说的堆指的是二叉堆。

二叉堆本质上是完全二叉树，可以分为两种类型：

• 最大堆（大顶堆）
• 最小堆（小顶堆）

二叉堆的根节点叫做 堆顶。最大堆和最小堆的特点，决定了在最大堆的堆顶是整个堆中的 最大元素；最小堆的堆顶是整个堆中的 最小元素。

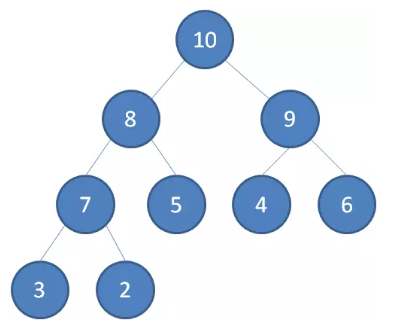
最大堆

最大堆任何一个父节点的值，都 大于等于 它左右孩子节点的值。

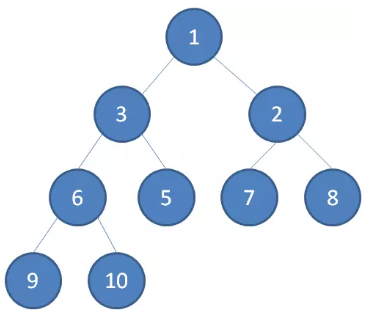
最小堆

最小堆任何一个父节点的值，都 小于等于 它左右孩子节点的值。

堆的逻辑结构与物理存储

二叉堆在逻辑上虽然是一颗完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组当中。

树的节点是按从上到下、从左到右的顺序紧凑排列的。

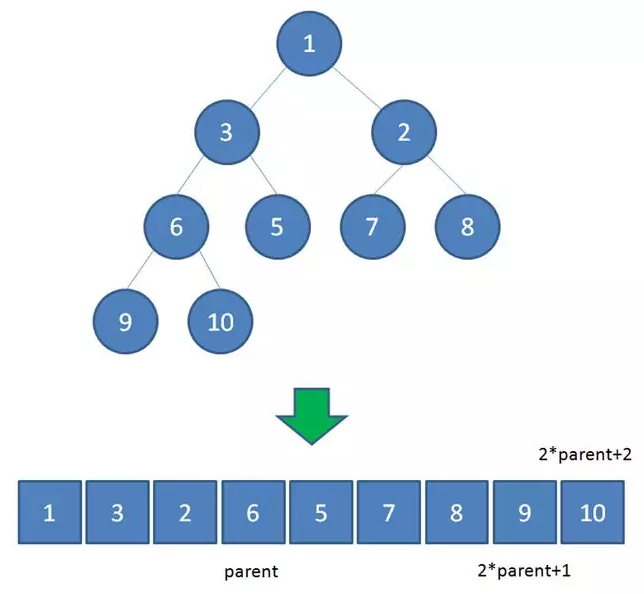
利用数组下标作为节点编号，假设父节点的下标是 parent，则有

• 左儿子的下标 = 2 * parent + 1
• 右儿子的下标 = 2 * parent + 2

堆的操作

对于堆，有两种主要操作：

• 插入节点 push

• 删除节点 pop

这两种操作都是基于堆的自我调整完成的。

堆的操作的复杂度

堆的插入和删除两种操作所花的时间和树的深度正比。

因此，如果一共有 \(n\) 个元素，那么堆的深度为 \(logn\)，则每个操作可以在 \(O(logn)\) 的时间完成。

堆的自我调整

以最小堆为例，看看堆是如何进行自我调整的：

插入节点

二叉堆的节点插入，插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点，值是 0。

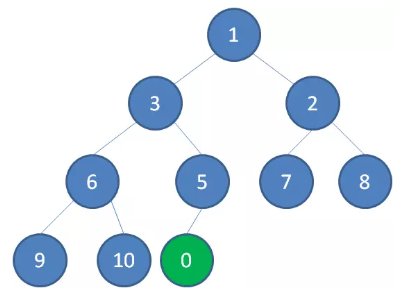
这时候，我们让节点 0 的它的父节点 5 做比较，如果 0 小于 5，则让新节点“上浮”，和父节点交换位置。

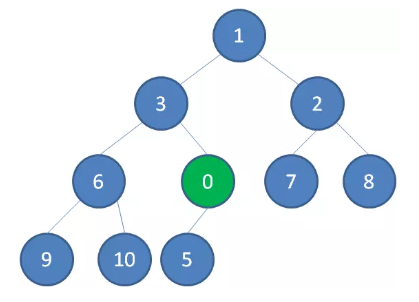
继续用节点 0 和父节点 3 做比较，如果 0 小于 3，则让新节点继续“上浮”。

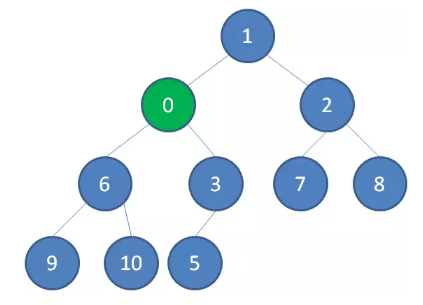
继续比较，最终让新节点 0 上浮到了堆顶位置。

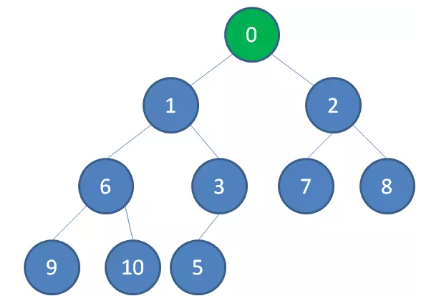
删除节点

二叉堆的节点删除过程和插入过程相反，所删除的是处于堆顶的节点。比如我们删除最小堆的堆顶节点 1。

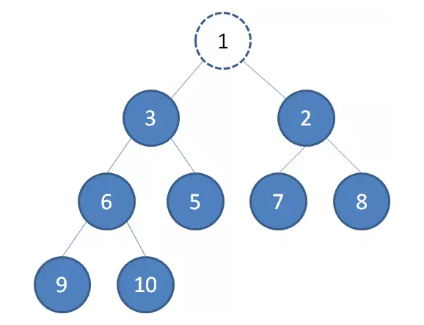
这时候，为了维持完全二叉树的结构，我们把堆的最后一个节点 10 补到原本堆顶的位置。

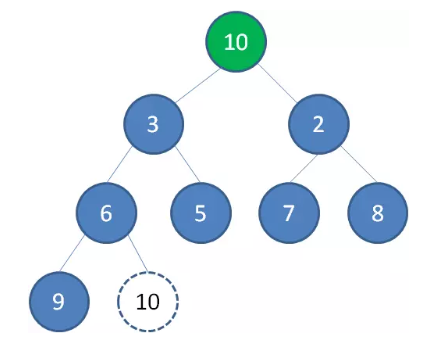
接下来我们让移动到堆顶的节点 10 和它的左右孩子进行比较，如果左右孩子中最小的一个（显然是节点 2 ）比节点 10 小，那么让节点 10 “下沉”。

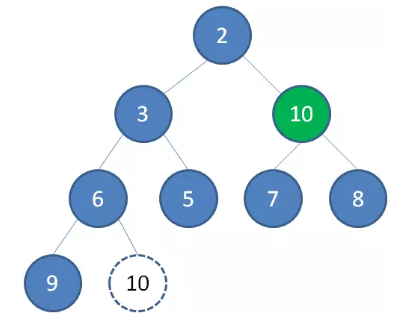
继续让节点 10 和它的左右孩子做比较，左右孩子中最小的是节点 7 ，由于 10 大于 7 ，让节点 10 继续“下沉”。

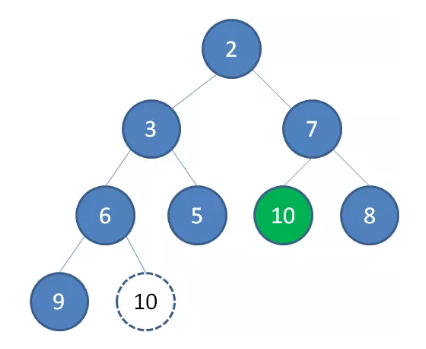
这样一来，堆重新得到了调整。

从上面的分析可知，显然不管是插入还是删除操作，堆的自我调整都与深度成正比，故时间复杂度为 \(O(logn)\)。

参考实现

最小堆参考实现，最大堆类似

public class MinimumHeap {

    private int[] heap;
    private int size = 0;

    /**
     * Creates a heap of specified capacity
     * @param heapMaxSize The maximum capacity of the initialization heap
     */
    public MinimumHeap(int heapMaxSize){
        heap = new int[heapMaxSize];
    }

    /**
     * floating
     * @param i Index of its own node
     * @param x The value to insert
     */
    private void floating(int i, int x){
        while (i > 0){
            //父节点的索引下标
            int p = (i - 1) / 2;
            //如果已经没有大小颠倒则退出
            if(heap[p] <= x) break;
            //把父亲节点的数值放下来，而把自己提上去
            heap[i] = heap[p];
            i = p;
        }
        heap[i] = x;
    }

    /**
     * sinking
     * @param x The value to move to the root
     */
    private void sinking(int x){
        int i = 0;
        while (i * 2 + 1 < size){
            //比较子节点的值
            int a = i * 2 + 1, b = i * 2 + 2;
            if(b < size && heap[b] < heap[a]) a = b;
            //如果已经没有大小颠倒则退出
            if(heap[a] >= x) break;
            //把子节点的数值提上来
            heap[i] = heap[a];
            i = a;
        }
        heap[i] = x;
    }

    public void push(int x){
        floating(size++, x);
    }

    public int pop(){
        int res = heap[0];
        sinking(heap[--size]);
        return res;
    }

    public int top(){
        return heap[0];
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public static void main(String[] args){
        int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
        MinimumHeap heap = new MinimumHeap(arr.length + 1);
        for (int e: arr) heap.push(e);
        while (!heap.isEmpty()){
            System.out.print(heap.pop() + " ");
        }
        //Output: -5 -4 -2 1 2 3 7 10
    }
}

堆排序

构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让 所有非叶子节点依次下沉。

我们举一个无序完全二叉树的例子：

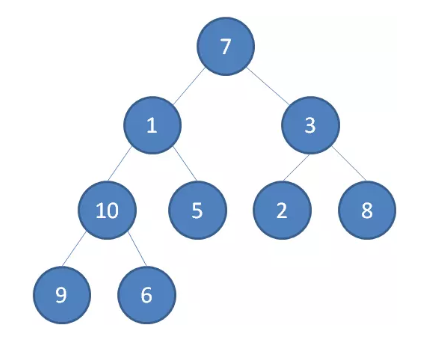
首先，我们从最后一个 非叶子 节点开始，也就是从节点 10 开始。如果节点 10 大于它左右孩子中最小的一个，则节点 10 下沉。

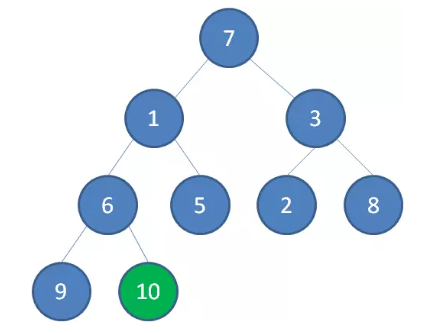
接下来轮到节点 3 ，如果节点 3 大于它左右孩子中最小的一个，则节点 3 下沉。

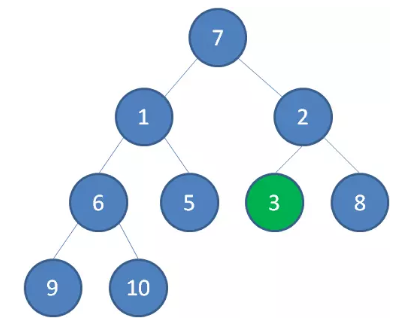
接下来轮到节点 1 ，如果节点 1 大于它左右孩子中最小的一个，则节点 1 下沉。事实上节点 1 小于它的左右孩子，所以不用改变。

接下来轮到节点 7 ，如果节点 7 大于它左右孩子中最小的一个，则节点 7 下沉。

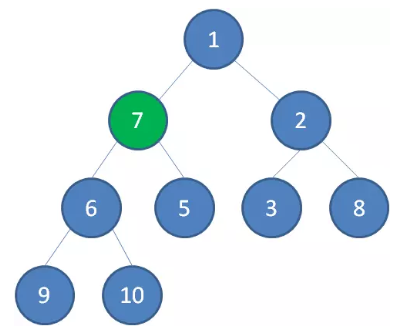
节点 7 继续比较，继续下沉。

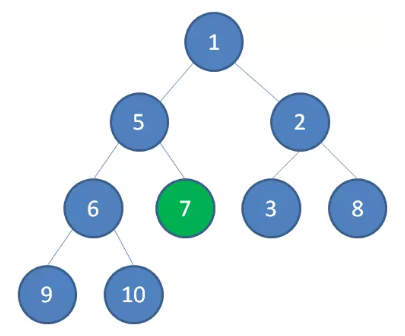
至此，一颗无序的完全二叉树就构建成了一个最小堆。

堆排序过程

堆排序是利用堆的自我调整实现的。

例如给定一个数组，对数组进行排序，使数组元素从小到大排列。

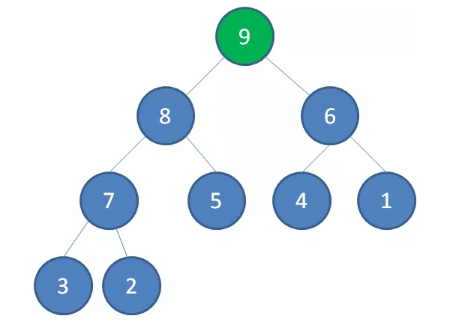
首先，我们要根据给定的数组构建一个最大堆。当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

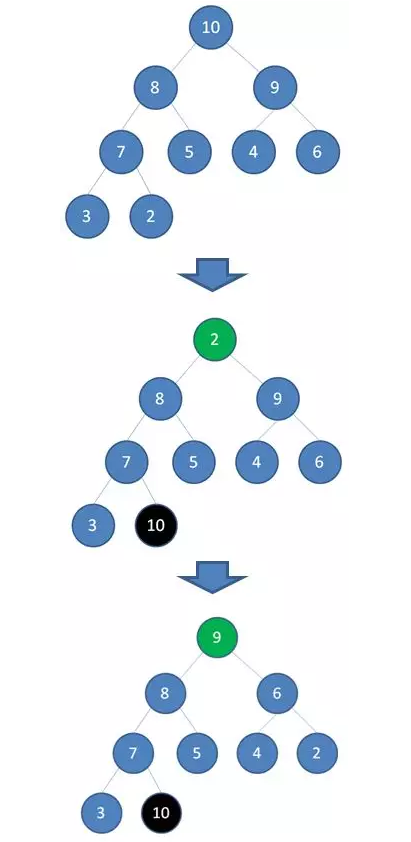
如上图所示，当删除值为 10 的堆顶节点，经过调节，值为 9 的新节点就会顶替上来；当删除值为 9 的堆顶节点，经过调节，值为 8 的新节点就会顶替上来.......

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

删除节点 9 ，节点 8 成为新堆顶：

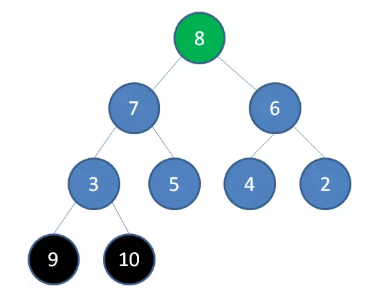
删除节点 8 ，节点 7 成为新堆顶：

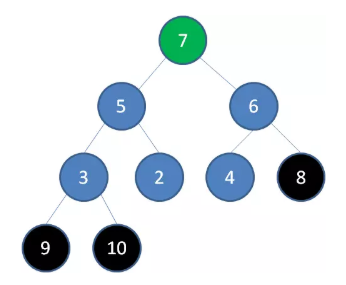
删除节点 7 ，节点 6 成为新堆顶：

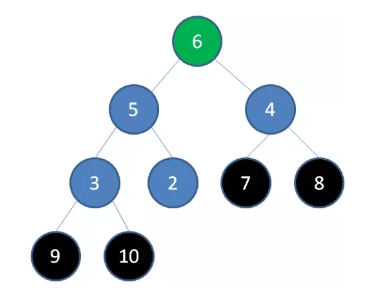
删除节点 6 ，节点 5 成为新堆顶：

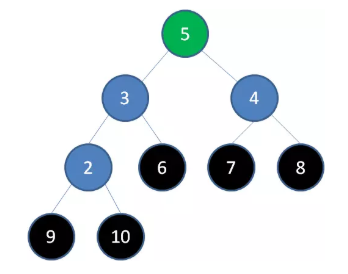
删除节点 5 ，节点 4 成为新堆顶：

删除节点 4 ，节点 3 成为新堆顶：

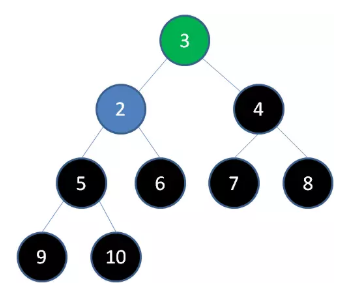
删除节点 3 ，节点 2 成为新堆顶：

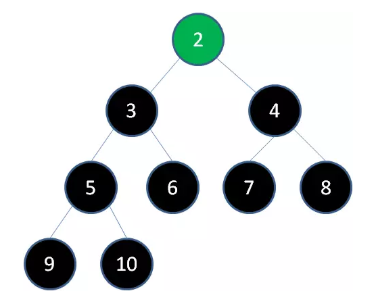
至此，原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

算法步骤

• 根据无序数组构建二叉堆
• 循环删除堆顶元素，移到数组尾部，调节堆产生新的堆顶

参考实现

import java.util.Arrays;

public class MaximumHeapSort {

    public static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    /**
     * sinking
     * @param heap The Heap to be adjusted
     * @param i The index of value which need to be sunk
     * @param x The value to be sunk
     * @param size The current valid size of heap
     */
    private static void sinking(int[] heap, int i, int x, int size){
        while (i * 2 + 1 < size){
            int a = i * 2 + 1, b = i * 2 + 2;
            //定位到最大的孩子节点
            if(b < size && heap[b] > heap[a]) a = b;
            //如果当前节点大于等于最大孩子节点，说明调整完毕
            if(heap[a] <= x) break;
            heap[i] = heap[a];
            i = a;
        }
        heap[i] = x;
    }

    /**
     * Build a heap according to an array
     * @param arr An array to form a heap
     */
    private static void buildHeap(int[] arr){
        for (int i = arr.length / 2 - 1; i >= 0; i--){
            sinking(arr, i, arr[i], arr.length);
        }
    }

    /**
     * Heap sort
     * @param arr Unsorted array
     */
    public static void sort(int[] arr){
        //根据无序数组构建二叉堆
        buildHeap(arr);
        //循环删除堆顶元素，移到数组尾部，调节堆产生新的堆顶
        for (int i = arr.length - 1; i > 0; i--){
            //最后一个元素和堆顶元素交换
            swap(arr, i, 0);
            //下沉调整最大堆
            sinking(arr, 0, arr[0], i);
        }
    }

    public static void main(String[] args){
        int[] arr = new int[]{10, 8, 9, 7, 5, 4, 6, 3, 2};
        MaximumHeapSort.sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

堆排序的复杂度

• 空间复杂度

  因为没有开辟额外的集合空间，所以空间复杂度为 \(O(1)\)

• 时间复杂度

  堆排序所需要的时间主要有两部分组成，一是构建二叉堆的时间，二是循环删除并进行堆维护的时间。

  • 第一步，把无序数组构建成二叉堆，需要进行 \(n/2\) 次循环。每次循环调用一次 sinking 方法，所以第一步的计算规模是 \((n/2) * logn\)，时间复杂度 \(O(nlogn)\)。

    这里只是初略地把每个非叶子节点下沉的时间复杂度都当成 \(O(logn)\) ，事实上经过严格的证明构建堆的时间复杂是 \(O(n)\) ，但这里我们初略算出的复杂度为 \(O(nlogn)\) ，当然我们算出的复杂度也是正确的，只不过是不够精确而已。

    \(O(n)\) 的证明也比较简单，可以参考：

    https://blog.csdn.net/LinuxTiger/article/details/7172258

  • 第二步，需要进行 \(n-1\) 次循环。每次循环调用一次 sinking 方法，所以第二步的计算规模是 \((n-1)*logn\) ，时间复杂度 \(O(nlogn)\) 。

  总的时间复杂度为： \[ O(n) + O(nlogn) = O(nlogn) \]

堆排序和快排对比

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
堆排序	\(O(nlogn)\)	\(O(nlogn)\)	\(O(nlogn)\)	\(O(1)\)	不稳定
快速排序	\(O(nlogn)\)	\(O(nlogn)\)	\(O(n^2)\)	\(O(logn) \sim O(n)\)	不稳定

• 相同点
  • 堆排序和快速排序的平均时间复杂度都是 \(O(nlogn)\)
  • 两者都是不稳定的排序
  • 快速排序因为递归所以需要额外的空间开销 \(O(logn) \sim O(n)\) ；堆排序是就地排序，空间复杂度 \(O(1)\)
• 不同点
  • 堆排序在最好、最坏、平均情况下时间复杂度都是 \(O(nlogn)\) ；快排在最坏情况下是 \(O(n^2)\) ，最好情况下是 \(O(nlogn)\)

优先队列

优先队列种类

优先队列不再遵循队列先入先出 (FIFO) 的原则，而是分为两种情况：

• 最大优先队列，无论入队顺序，当前最大的元素优先出队。
• 最小优先队列，无论入队顺序，当前最小的元素优先出队。

比如有一个最大优先队列，它的最大元素是 8 ，那么虽然元素 8 并不是队首元素，但出队的时候仍然让元素 8 首先出队：

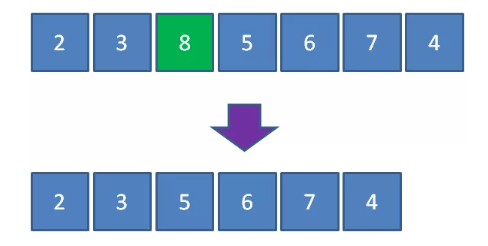
要满足以上需求，利用线性数据结构并非不能实现，但是时间复杂度较高，最坏时间复杂度 \(O(n)\)，并不是最理想的方式。

利用堆的特性实现优先队列

堆的特性：

• 最大堆的堆顶是整个堆中的最大元素
• 最小堆的堆顶是整个堆中的最小元素

因此，可以用最大堆来实现最大优先队列，最小堆实现最小优先队列。

例如，利用最大堆实现优先队列，每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点。

入队操作

插入新节点 5

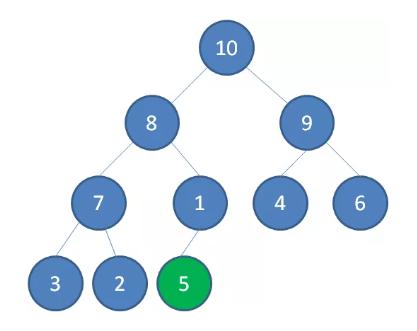
新节点 5 上浮到合适位置

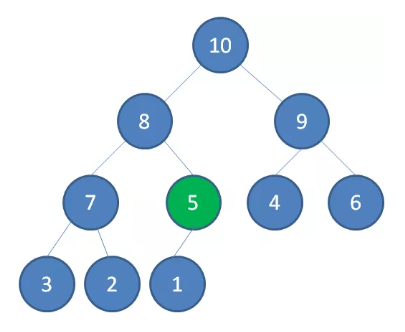
出队操作

把原堆顶节点 10 “出队”

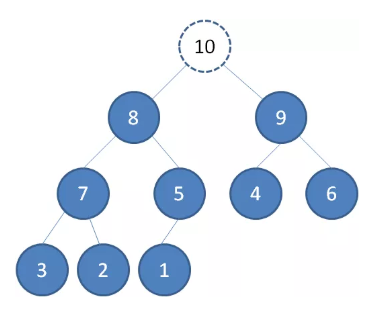
最后一个节点 1 替换到堆顶位置

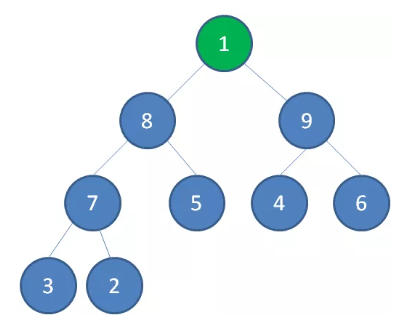
节点1下沉，节点 9 成为新堆顶

优先队列的时间复杂度

因为二叉堆节点上浮和下沉的时间复杂度都是 \(O(logn)\) ，所以优先队列入队和出队的时间复杂度也是 \(O(logn)\)

参考实现

import java.util.Arrays;

public class PriorityQueue {

    private static final int DEFAULT_CAPACITY = 16;

    private int[] queue;
    private int size;

    /**
     * Constructs an empty queue with the default capacity.
     */
    public PriorityQueue(){
        this.size = 0;
        this.queue = new int[DEFAULT_CAPACITY];
    }

    /**
     * Constructs an empty queue with the specified initial capacity.
     * @param capacity the initial capacity of the queue
     */
    public PriorityQueue(int capacity){
        this.size = 0;
        this.queue = (capacity > 0) ? new int[capacity] : new int[DEFAULT_CAPACITY];
    }

    /**
     * floating
     * @param i Index of its own node
     * @param x The value to insert
     */
    private void floating(int i, int x){
        while (i > 0){
            int p = (i - 1) / 2;
            if(queue[p] >= x) break;
            queue[i] = queue[p];
            i = p;
        }
        queue[i] =  x;
    }

    /**
     * sinking
     * @param x The value to move to the root
     */
    private void sinking(int x){
        int i = 0;
        while (2 * i + 1 < size){
            int a = 2 * i + 1, b = 2 * i + 2;
            if(b < size && queue[b] > queue[a]) a = b;
            if(queue[a] <= x) break;
            queue[i] = queue[a];
            i = a;
        }
        queue[i] = x;
    }

    /**
     * Increases the capacity of the queue
     */
    private void resize(){
        this.queue = Arrays.copyOf(this.queue, this.size * 2);
    }

    public void push(int x){
        if(size == queue.length) resize();
        floating(size++, x);
    }

    public int pop(){
        int res = queue[0];
        sinking(queue[--size]);
        return res;
    }

    public int front(){
        return queue[0];
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public static void main(String[] args){
        int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
        PriorityQueue queue = new PriorityQueue();
        for (int e: arr) queue.push(e);
        while (!queue.isEmpty()){
            System.out.print(queue.pop() + " ");
        }
    }
}

References

https://en.wikipedia.org/wiki/Heap_(data_structure)

https://mp.weixin.qq.com/s/23CwW5eSv-lI6vaZHzSwhQ

https://mp.weixin.qq.com/s/PWuuChodYGMr8iJzW2VW9Q

https://mp.weixin.qq.com/s/CdK1l2kB3aCUtBORjS4DVQ