HeapSort

在计算机科学中，堆排序（Heapsort）是一种基于比较的排序算法。Heapsort 可以被认为是一种改进的选择排序：像该算法一样，它将输入分为排序区域和未排序区域，并通过提取最大元素并将其移动到排序区域来迭代缩小未排序区域。改进包括使用堆数据结构而不是线性时间搜索来找到最大值。

堆排序（Heapsort）

基本原理

传送门 堆、堆排序、优先队列

算法步骤

1. 由输入的无序数组构造一个最大堆，作为初始的无序区
2. 把堆顶元素（最大值）和堆尾元素互换
3. 把堆（无序区）的尺寸缩小 1 ，并调用 sinking 函数，目的是把新的数组顶端数据调整到相应位置
4. 重复步骤 2 ，直到堆的尺寸为 1

算法图解

构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让 所有非叶子节点依次下沉。

我们举一个无序完全二叉树的例子：

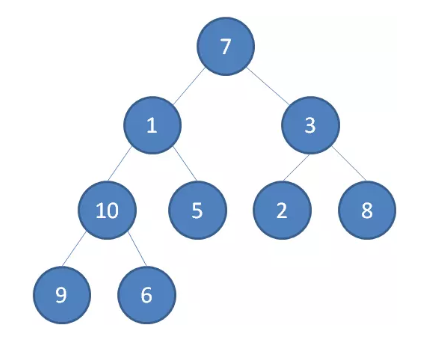
首先，我们从最后一个 非叶子 节点开始，也就是从节点 10 开始。如果节点 10 大于它左右孩子中最小的一个，则节点 10 下沉。

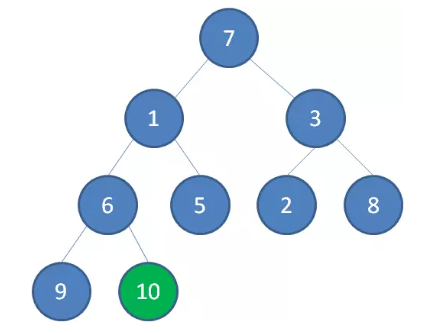
接下来轮到节点 3 ，如果节点 3 大于它左右孩子中最小的一个，则节点 3 下沉。

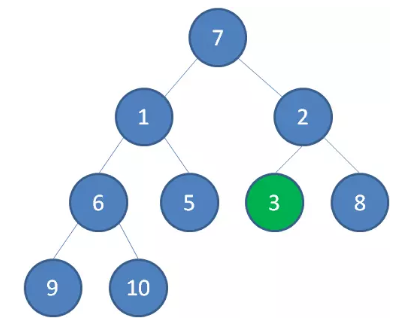
接下来轮到节点 1 ，如果节点 1 大于它左右孩子中最小的一个，则节点 1 下沉。事实上节点 1 小于它的左右孩子，所以不用改变。

接下来轮到节点 7 ，如果节点 7 大于它左右孩子中最小的一个，则节点 7 下沉。

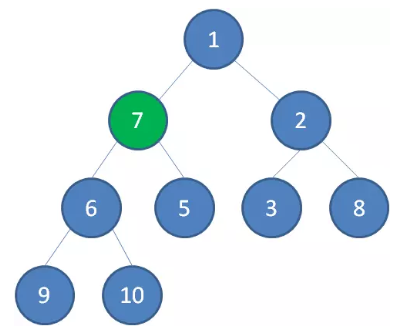
节点 7 继续比较，继续下沉。

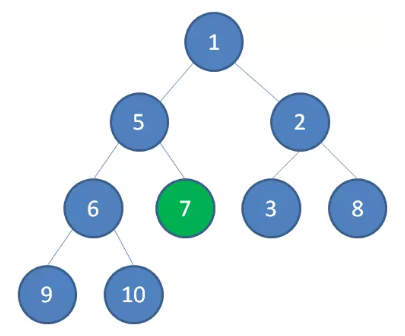
至此，一颗无序的完全二叉树就构建成了一个最小堆。

堆排序过程

堆排序是利用堆的自我调整实现的。

例如给定一个数组，对数组进行排序，使数组元素从小到大排列。

首先，我们要根据给定的数组构建一个最大堆。当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

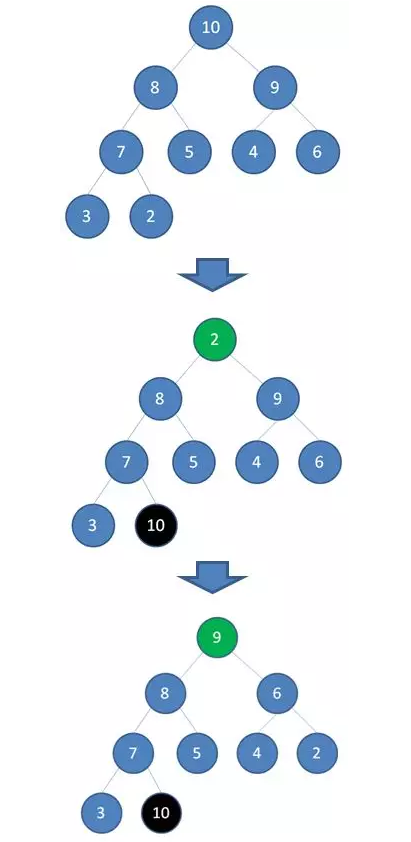
如上图所示，当删除值为 10 的堆顶节点，经过调节，值为 9 的新节点就会顶替上来；当删除值为 9 的堆顶节点，经过调节，值为 8 的新节点就会顶替上来.......

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

删除节点 9 ，节点 8 成为新堆顶：

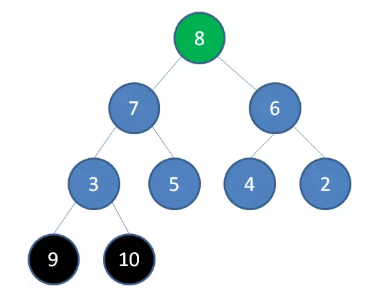
删除节点 8 ，节点 7 成为新堆顶：

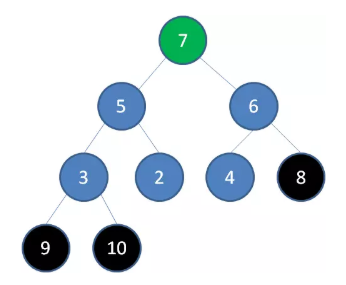
删除节点 7 ，节点 6 成为新堆顶：

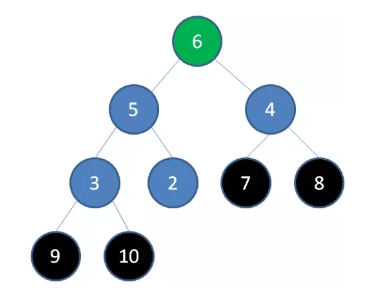
删除节点 6 ，节点 5 成为新堆顶：

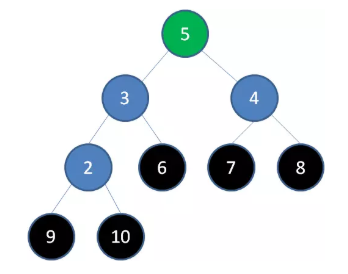
删除节点 5 ，节点 4 成为新堆顶：

删除节点 4 ，节点 3 成为新堆顶：

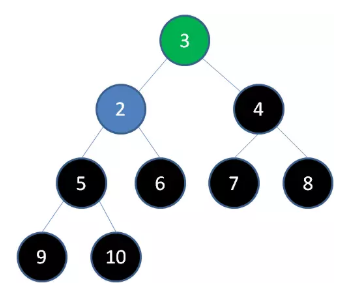
删除节点 3 ，节点 2 成为新堆顶：

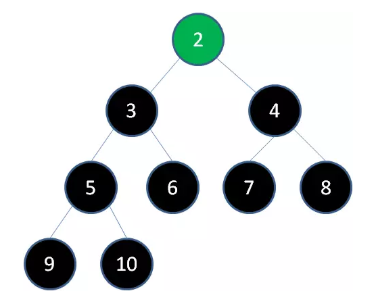
至此，原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

动画演示

参考实现

import java.util.Arrays;

/**
 * @author wylu
 */
public class HeapSort {

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    /**
     * 下沉操作
     * @param heap 需要调整的堆
     * @param i 需要下沉元素的索引
     * @param x 需要下沉元素的值
     * @param size 当前堆的有效范围
     */
    private static void sinking(int[] heap, int i, int x, int size) {
        while (2 * i + 1 < size) {
            int a = 2 * i + 1, b = 2 * i + 2;
            //定位到最大的孩子节点
            if (b < size && heap[b] > heap[a]) a = b;
            //如果当前节点大于等于最大孩子节点，说明调整完毕
            if (heap[a] <= x) break;
            heap[i] = heap[a];
            i = a;
        }
        heap[i] = x;
    }

    /**
     * 构建大顶堆
     * @param arr 建堆数组
     */
    private static void buildMaxHeap(int[] arr) {
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            sinking(arr, i, arr[i], arr.length);
        }
    }

    public static void sort(int[] arr) {
        //根据无序数组构建二叉堆
        buildMaxHeap(arr);
        //循环删除堆顶元素，移到数组尾部，调节堆产生新的堆顶
        for (int i = arr.length - 1; i > 0; i--) {
            //最后一个元素和堆顶元素交换
            swap(arr, i, 0);
            //下沉调整最大堆
            sinking(arr, 0, arr[0], i);
        }
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 4, 9, 6, 0, 7, 2, 5, 8};
        HeapSort.sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

复杂度分析

排序算法	平均时间复杂度	最好情况	最坏情况	空间复杂度	排序方式	稳定性
堆排序	\(O(nlogn)\)	\(O(nlogn)\)	\(O(nlogn)\)	\(O(1)\)	In-place	不稳定

References

https://en.wikipedia.org/wiki/Heapsort

https://blog.csdn.net/qq_32767041/article/details/83352265

https://youliao.163yun.com/api-server/rss/xiaomi/item/IN2WDOMKAWVNTZV.html?ref=browser_news&s=mb&cp=cn-netease-youliao-browser&docid=44797c69e120935b2c4790d933d02a9b&itemtype=news&cateCode=rec&category=%E7%A7%91%E6%8A%80